“一带一路”的战略构想为国内许多企业的发展带来了新的机遇，某公司生产 ， 两种机械设备，每台 种设备的成本是 种设备的1.5倍，公司若投入16万元生产 种设备，36万元生产 种设备，则可生产两种设备共10台．请解答下列问题：
（1） 、 两种设备每台的成本分别是多少万元？
（2）若 ， 两种设备每台的售价分别是6万元，10万元，公司决定生产两种设备共60台，计划销售后获利不低于126万元，且 种设备至少生产53台，求该公司有几种生产方案；
（3）在（2）的条件下，销售前公司决定从这批设备中拿出一部分，赠送给“一带一路”沿线的甲国，剩余设备全部售出，公司仍获利44万元，赠送的设备采用水路运输和航空运输两种方式，共运输4次，水路运输每次运4台 种设备，航空运输每次运2台 种设备（运输过程中产生的费用由甲国承担）．直接写出水路运输的次数．
如图，⊙M经过O点，并且⊙M与x轴，y轴分别交于A，B两点，线段OA，OB（OA＞OB）的长是方程
的两根．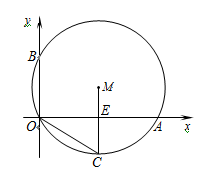
（1）求线段OA，OB的长；
（2）已知点C是劣弧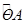
的中点，连结MC交OA轴于点E．
①判断MC与OA的位置关系，并说明理由；
②求点C的坐标．
已知某商品的进价为每件30元，九（1）班数学兴趣小组经过市场调查，整理出该商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：
| 第x天 |
1≤x＜50 |
50≤x≤90 |
| 售价（元/件） |
x＋40 |
90 |
| 每天销量（件） |
200－2x |
（1）分别求出第25天和第60天商家在销售该商品时所获得的利润；
（2）问销售该商品第几天时，当天的销售利润为6050元？
如图，AC是⊙O的直径，点B、D在⊙O上，点E在⊙O外，∠EAB＝∠D＝30°．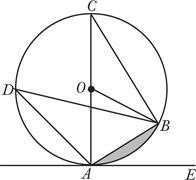
（1）∠C的度数为 °；
（2）判断直线AE与⊙O的位置关系，并说明理由；
（3）当AB＝2时，求图中阴影部分的面积（结果保留根号和π）．
滨海县为创建“文明卫生城市”，积极投入资金进行城市道路建设与园林绿化两项工程，已知2012年投资1000万元，预计2014年投资1210万元．若这两年内平均每年投资增长的百分率相同．
（1）求平均每年投资增长的百分率；
（2）按此增长率，计算2015年投资额能否达到1360万元？
一分钟投篮测试规定：满分为10分，成绩达到6分及以上为合格，成绩达到8分及以上为优秀．甲、乙两组各15名学生的某次测试成绩如下：
| 成绩 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 甲组（人） |
0 |
0 |
0 |
2 |
6 |
3 |
0 |
2 |
2 |
0 |
| 乙组（人） |
0 |
0 |
0 |
2 |
2 |
8 |
1 |
1 |
1 |
0 |
（1）请补充完成下面的成绩分析表：
| 统计量 |
平均分 |
方差 |
中位数 |
众数 |
合格率 |
优秀率 |
| 甲组 |
 |
5 |
46．7% |
|||
| 乙组 |
6 |
 |
6 |
73．3% |
13．3% |
（2）你认为甲、乙两组哪一组的投篮成绩较好？请写出支持你的观点的理由．