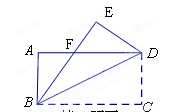
如图, 中, , . 是底边 上的一个动点 与 、 不重合),以 为圆心, 为半径的 与射线 交于点 ,射线 交射线 于点 .
(1)若点 在线段 的延长线上,设 , ,求 关于 的函数关系式,并写出 的取值范围.
(2)当 时,试说明射线 与 是否相切.
(3)连接 ,若 ,求 的长.

注意:为了使同学们更好地解答本题,下面提供了一种解题思路,你可以依照这个思路,完成本题的解答过程.如果你选用其他的解题方案进行解答也可.
如图①,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?
分析:由横、竖彩条的宽度比为2∶3,可设每个横彩条的宽为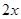 ,则每个竖彩条的宽为
,则每个竖彩条的宽为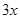 .为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形
.为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形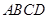 .结合以上分析列出方程并完成本题解答.
.结合以上分析列出方程并完成本题解答.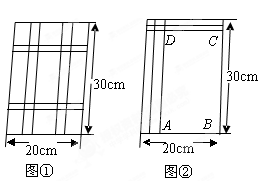
如图,在梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.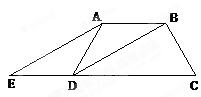
(1)求证:梯形ABCD是等腰梯形.
(2)若∠BDC=30°,AD=5,求CD的长.
随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2007年底拥有家庭轿车64辆,2009年底家庭轿车的拥有量达到100辆.若该小区2007年底到2010年底家庭轿车拥有量的年平均增长率都相同,求该小区到2010年底家庭轿车将达到多少辆?
如图,已知BE⊥AD,CF⊥AD,且BE=CF.试判断AD是△ABC的中线还是角平分线?请证明你的结论.
连接BF、CE,若四边形BFCE是菱形,则△ABC中应添加的一个条件是

如图,把一张矩形纸片ABCD沿对角线BD对折,使点C落在点E处,BE与AD交于点F.试判断重合部分图形的形状,并说明理由.