我国古代数学家利用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是

A. B.
B.
C. D.
D.
函数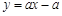 与
与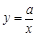 (a≠0)在同一直角坐标系中的图象可能是( )
(a≠0)在同一直角坐标系中的图象可能是( )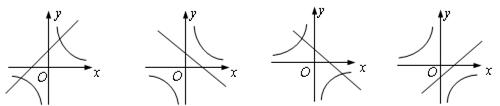
A. B. C. D.
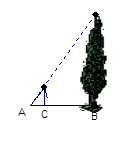
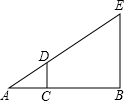
如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米 , CA=1米, 则树的高度为()
| A. 4.5米 | B. 6米 | C.3米 | D. 4米 |
已知粉笔盒里只有2支黄色粉笔和3支红色粉笔,每支粉笔除颜色外均相同,现从中任取一支粉笔,则取出黄色粉笔的概率是( )
A. |
B.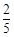 |
C. |
D. |
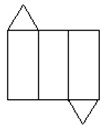
右图可以折叠成的几何体是( )
| A.三棱柱 | B.四棱柱 | C.圆柱 | D.圆锥 |
观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有( )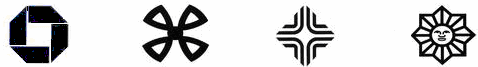
| A.1个 | B.2个 | C.3个 | D.4个 |