在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一: |
68 |
88 |
100 |
100 |
79 |
94 |
89 |
85 |
100 |
88 |
100 |
90 |
98 |
97 |
77 |
94 |
96 |
100 |
92 |
67 |
|
初二: |
69 |
97 |
96 |
89 |
98 |
100 |
99 |
100 |
95 |
100 |
99 |
69 |
97 |
100 |
99 |
94 |
79 |
99 |
98 |
79 |
(1)根据上述数据,将下列表格补充完成.
整理、描述数据:
分数段 |
|
|
|
|
初一人数 |
2 |
2 |
4 |
12 |
初二人数 |
2 |
2 |
1 |
15 |
分析数据:样本数据的平均数、中位数、满分率如表:
年级 |
平均数 |
中位数 |
满分率 |
初一 |
90.1 |
93 |
|
初二 |
92.8 |
|
|
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 人;
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
图①中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图②.在图②中,每个菱形的边长为10cm,锐角为60°.
(1)连接CD,EB,猜想它们的位置关系并加以证明;
(2)求A,B两点之间的距离(结果取整数,可以使用计算器).
(参考数据: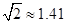 ,
,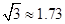 ,
,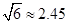 )
)
如图,为了知道空中一静止的广告气球A的高度,小宇在B处测得气球A的仰角为18°,他向前走了20m到达C处后,再次测得气球A的仰角为45°,已知小宇的眼睛距离地面1.6m,求此时气球A距离地面的高度(结果精确到0.1m,参考数据:tan18°≈0.3249).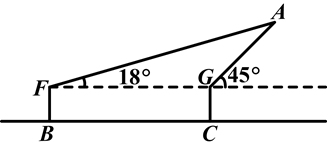
在△ABC中,AD是BC边上的高,∠C=45°, ,AD=1.求BC的长.
,AD=1.求BC的长.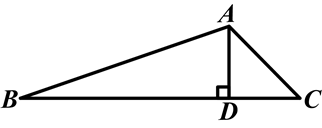
一辆汽车从B处出发,沿斜坡爬行30米到达A处,若坡度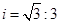 ,求坡角α和汽车上升的高度h.
,求坡角α和汽车上升的高度h.
如图所示,某校九年级(3)班的一个学习小组进行测量小山高度的实践活动.部分同学在山脚A点处测得山腰上一点D的仰角为30°,并测得AD的长度为180米.另一部分同学在山顶B点处测得山脚A点的俯角为45°,山腰D点的俯角为60°,请你帮助他们计算出小山的高度BC.(计算过程和结果都不取近似值)