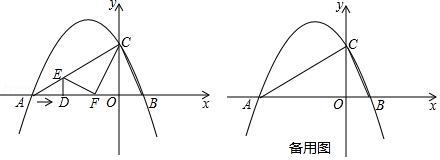
如图,抛物线 与 轴交于两点 和 ,与 轴交于点 ,动点 沿 的边 以每秒2个单位长度的速度由起点 向终点 运动,过点 作 轴的垂线,交 的另一边于点 ,将 沿 折叠,使点 落在点 处,设点 的运动时间为 秒.
(1)求抛物线的解析式和对称轴;
(2)是否存在某一时刻 ,使得 为直角三角形?若存在,求出 的值;若不存在,请说明理由;
(3)设四边形 的面积为 ,求 关于 的函数表达式.
比较-3与2的大小.
如图所示,数轴上标出若干个点,每相邻两点相距一个单位长度,点A,B,C,D对应的数分别是数a,b,c,d,且d-2a=10,那么数轴的原点应是哪一点?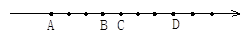
比较a与-a的大小.
超市、书店、玩具店依次坐落在一条东西走向的大街上,超市在书店西边20米处,玩具店位于书店东边50米处.小明从书店出来沿街向东走了50米,接着又向东走了-80米,此时小明的位置在何处?在数轴上标出超市、书店、玩具店的位置,以及小明最后的位置.
初一(4)班在一次联欢活动中,把全班分成5个队参加活动,游戏结束后,5个队的得分如下:
A队:-50分;B队:150分;C队:-300分;D队:0分;E队:100分.
(1)将5个队按由低分到高分的顺序排序;
(2)把每个队的得分标在数轴上,并将代表该队的字母标上;
(3)从数轴上看A队与B队相差多少分?C队与E队呢?