如图，抛物线y23x2bxc经过点B(3,0)，C(0,−2-优题课

题文

如图，抛物线 $y = \frac{2}{3} x^{2} + bx + c$ 经过点 $B (3, 0)$ ， $C (0, - 2)$ ，直线 $l : y = - \frac{2}{3} x - \frac{2}{3}$ 交 $y$ 轴于点 $E$ ，且与抛物线交于 $A$ ， $D$ 两点， $P$ 为抛物线上一动点（不与 $A$ ， $D$ 重合）．

（1）求抛物线的解析式；

（2）当点 $P$ 在直线 $l$ 下方时，过点 $P$ 作 $PM / / x$ 轴交 $l$ 于点 $M$ ， $PN / / y$ 轴交 $l$ 于点 $N$ ，求 $PM + PN$ 的最大值．

（3）设 $F$ 为直线 $l$ 上的点，以 $E$ ， $C$ ， $P$ ， $F$ 为顶点的四边形能否构成平行四边形？若能，求出点 $F$ 的坐标；若不能，请说明理由．

科目数学题型解答题难度较难

知识点：二次函数的性质待定系数法求二次函数解析式二次函数综合题

登录免费查看答案和解析

相关试题

计算：

如图，抛物线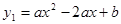的顶点为D，与x轴交于点A，B，与y轴交于点C，且OB =" 2OC=" 3．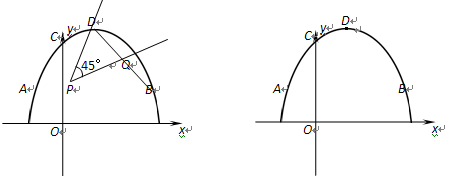

（1）求a，b的值；
（2）将45°角的顶点P在线段OB上滑动(不与点B重合)，该角的一边过点D，另一边与BD交于点Q，设P（x，0），y₂=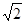DQ，试求出y₂关于x的函数关系式；
（3）在同一平面直角坐标系中，两条直线x = m，x = m+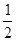分别与抛物线y₁交于点E，G，与y₂的函数图象交于点F，H．问点E、F、H、G围成四边形的面积能否为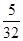？若能，求出m的值；若不能，请说明理由．

△ABC中，∠A=90°，点D在线段BC上（端点B除外），∠EDB = 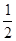∠C，BE⊥DE于点E，DE与AB相交于点F．
（1）当AB = AC时（如图1）
①∠EBF=　▲　°；
②小明在探究过程中发现，线段FD 与BE始终保持一种特殊的数量关系，请你猜想这个关系，并利用所学知识证明猜想的正确性；
（2）探究：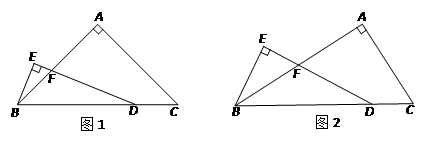

当AB = kAC时（k＞0，如图2），用含k的式子表示线段FD与BE之间的数量关系，请直接写出结果．

如图，C为以AB为直径的⊙O上一点，AD和过点C的切线互相垂直，垂足为点D．

（1）求证：AC平分∠BAD；
（2）若CD3，AC=3，求⊙O的半径长．

如图，过点B（2，0）的直线l：交y轴于点A，与反比例函数的图象交于点C（3，n）．、

（1）求反比例函数的解析式；
（2）将△OBC绕点O逆时针方向旋转α角（α为锐角），
得到△OB′C′．当OC′⊥AB时，求点C运动的路径长．

试卷网试题网古诗词网作文网范文网