如图,抛物线 与 轴交于 , 两点(点 在点 左侧),与 轴交于点 ,点 是抛物线上的一个动点,且位于第四象限,连接 、 、 、 ,延长 交 轴于点 .
(1)若 为等腰直角三角形,求 的值;
(2)若对任意 , 、 两点总关于原点对称,求点 的坐标(用含 的式子表示);
(3)当点 运动到某一位置时,恰好使得 ,且点 为线段 的中点,此时对于该抛物线上任意一点 , 总有 成立,求实数 的最小值.

某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院慰问孤寡老人,如果给每个老人分5盒,则剩下38盒,如果给每个老人分6盒,则最后一个老人不足5盒,但至少分得一盒.
(1)设敬老院有x名老人,则这批牛奶共有多少盒?(用含x的代数式表示).
(2)该敬老院至少有多少名老人?最多有多少名老人?
某市为争创全国文明卫生城,2008年市政府对市区绿化工程投入的资金是2000万元,2010年投入的资金是2420万元,且从2008年到2010年,两年间每年投入资金的年平均增长率相同.
(1)求该市对市区绿化工程投入资金的年平均增长率;
(2)若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?
“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:
(1)这次抽查的家长总人数为 100 ;
(2)请补全条形统计图和扇形统计图;
(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率是 .
.
求证:角平分线上的点到这个角的两边距离相等.
已知:
求证:
证明:
解二元一次方程组: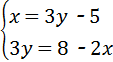 .
.