参照学习函数的过程与方法,探究函数 的图象与性质.
因为 ,即 ,所以我们对比函数 来探究.
列表:
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
1 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
2 |
3 |
5 |
|
|
0 |
|
|
|
描点:在平面直角坐标系中,以自变量 的取值为横坐标,以 相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把 轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当 时, 随 的增大而 ;(填“增大”或“减小”
② 的图象是由 的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3)设 , , , 是函数 的图象上的两点,且 ,试求 的值.
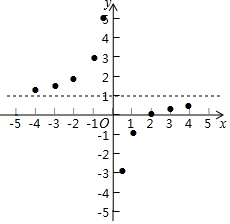
为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容.为了了
解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制
统计图如下:
请根据统计图提供的信息回答以下问题:
(1)抽取的学生数为_______名;
(2)该校有3000名学生,估计喜欢收听易中天《品三国》的学生有_______名;
(3)估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的____%;
(4)你认为上述估计合理吗?理由是什么?
(Ⅰ)某服装厂承揽一项生产夏凉小衫1600件的任务,计划用
天完成.
(1)写出每天生产夏凉小衫
(件)与生产时间
(天)(
)之间的函数关系式;
(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?
(Ⅱ)如图,已知矩形
中,
是
上的一点,
是
上的一点,
,且
,
,矩形
的周长为32cm,求
的长.

(1)(本小题满分4分)计算: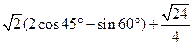 .
.
(2)(本小题满分6分)
进入防汛期后,某地对河堤进行了加固.该地驻军在河堤加固的工程中出色完成了任务.这
是记者与驻军工程指挥官的一段对话:
通过这段对话,请你求出该地驻军原来每天加固的米数.
如图9,抛物线 与
与 轴交于A、B两点,与
轴交于A、B两点,与 轴交于点C(0,
轴交于点C(0, ).
).
(1)求抛物线的对称轴及 的值;
的值;
(2)抛物线的对称轴上存在一点P,使得 的值最小,求此时点P的坐标;
的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标;
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.
某电器城经销A型号彩电,今年四月份每台彩电售价为2000元,与去年同期相比,结果卖出彩电的数量相同,但去年销售额为5万元,今年销售额只有4万元.
(1)问去年四月份每台A型号彩电售价是多少元?
(2)为了改善经营,电器城决定再经销B型号彩电.已知A型号彩电每台进货价为1800元,B型号彩电每台进货价为1500元,电器城预计用不多于 万元且不少于
万元且不少于 万元的资金购进这两种彩电共20台,问有哪几种进货方案?
万元的资金购进这两种彩电共20台,问有哪几种进货方案?
(3)电器城准备把A型号彩电继续以原价每台2000元的价格出售,B型号彩电以每台1800元的价格出售,在这批彩电全部卖出的前提下,如何进货才能使电器城获利最大?最大利润是多少?