“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买 、 两种型号的垃圾处理设备共10台.已知每台 型设备日处理能力为12吨;每台 型设备日处理能力为15吨;购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买 、 两种设备的方案;
(2)已知每台 型设备价格为3万元,每台 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
如图,在矩形ABCD中,E是CD边上的点,且BE=BA,以点A为圆心、AD长为半径作⊙A交AB于点M,过点B作⊙A的切线BF,切点为F.
(1)请判断直线BE与⊙A的位置关系,并说明理由;
(2)如果AB=10,BC=5,求图中阴影部分的面积.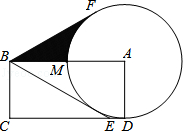
近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.
(1)求每台A种、B种设备各多少万元?
(2)根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC和△DEF的顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC向上平移4个单位长度后所得到的△A1B1C1;
(2)画出△DEF绕点O按顺时针方向旋转90°后所得到的△D1E1F1;
(3)△A1B1C1和△D1E1F1组成的图形是轴对称图形吗?如果是,请直接写出对称轴所在直线的解析式.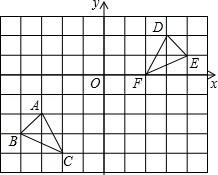
居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:
| A.非常赞同; | B.赞同但要有时间限制; | C.无所谓; | D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图. |

请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
先化简,再求值:(1- )÷
)÷ ,其中x=(
,其中x=( +1)0+(
+1)0+( )-1•tan60°.
)-1•tan60°.