某校在宣传“民族团结”活动中，采用四种宣传形式： ．器乐， ．舞蹈， ．朗诵， ．唱歌．每名学生从中选择并且只能选择一种最喜欢的，学校就宣传形式对学生进行了抽样调查，并将调查结果绘制了如下两幅不完整的统计图．
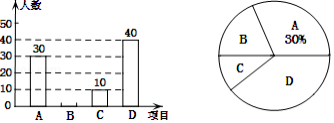
请结合图中所给信息，解答下列问题：
（1）本次调查的学生共有 人；
（2）补全条形统计图；
（3）该校共有1200名学生，请估计选择“唱歌”的学生有多少人？
（4）七年一班在最喜欢“器乐”的学生中，有甲、乙、丙、丁四位同学表现优秀，现从这四位同学中随机选出两名同学参加学校的器乐队，请用列表或画树状图法求被选取的两人恰好是甲和乙的概率．
如图，Rt△AOC中，∠ACO=90°，∠AOC=30°．将Rt△AOC绕OC中点E按顺时针方向旋转180°后得到Rt△BCO，BO、CO恰好分别在y轴、x轴上．再将Rt△BCO沿y轴对折得到Rt△BDO．取BC中点F，连接DF，交AB于点G，将△BDG沿DF对折得到△KDG．直线DK交AB于点H．
填空：CE:ED=________,AB:AC=__________；
若BH=
，求直线BD解析式在（2）的条件下，一抛物线过点D、点E、点B，此抛物线位于直线BD上方有一动点Q,△BDQ的面积有无最大值？若有，请求出点Q的坐标；若无，请说明理由
如图，AB、ED是⊙O的直径，点C在ED延长线上, 且∠CBD =∠FAB．点F在⊙O上，且 AB⊥DF．连接AD并延长交BC于点G．
求证：BC是⊙O的切线；
求证：BD·BC=BE·CD；
若⊙O 的半径为r，BC=3r，求tan∠CDG的值
阅读材料：已知p2－p－1＝0 , 1－q－q2＝0 , 且pq≠1 ,求
的值．
解：由p2－p－1＝0及1－q－q2＝0，可知p≠0，q≠0，
又因为pq≠1 所以p≠
，所以1－q－q2 =0可变形为：（）2－()－1＝0 ，
根据p2－p－1＝0和（）2－()－1＝0的特征，
p与可以看作方程x2－x－1＝0的两个不相等的实数根，所以p＋＝1,所以＝1．
根据以上阅读材料所提供的方法，完成下面的解答：已知m2-5mn+6n2=0，m>n，求
的值已知2m2－5m－1＝0，(
)2＋
－2＝0，且m≠n ，求
的值．
某商场销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=－10x+500．设商场每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
若物价部门规定，这种护眼台灯的销售单价不得高于32元，求该商场每月可获得最大利润．
如图，小岛A在港口P的南偏西45°方向，距离港口81海里处．甲船从A出发，沿AP方向以9海里/时的速度驶向港口，乙船从港口P出发，沿南偏东60°方向，以18海里/时的速度驶离港口，现两船同时出发．
出发后几小时两船与港口P的距离相等？
出发后几小时乙船在甲船的正东方向？（结果精确到0.1小时）
（参考数据：
≈1.41，
≈1.73）