在平面直角坐标系中,点 为坐标原点,抛物线 与 轴交于点 , ,与 轴交于点 ,顶点为 .
(1)求抛物线和直线 的解析式;
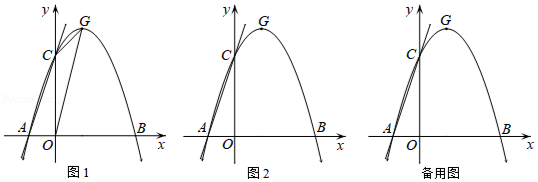
(2)如图1,设 为 轴上一动点,若 和 的面积满足 ,求点 的坐标;
(3)如图2,设点 从点 出发,以每秒1个单位长度的速度沿 轴向右运动,运动时间为 ,点 为射线 上一动点,过点 作 轴交抛物线对称轴右侧部分于点 .试探究点 在运动过程中,是否存在以 , , 为顶点的三角形为等腰直角三角形?若存在,求出 的值;若不存在,请说明理由.
计算:(前3题每小题4分,第(4)题6分,共18分)(1)

(2)
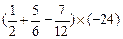
(3)
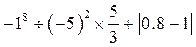
(4)先化简,再求值。
 ;其中a=—2,b=3
;其中a=—2,b=3
应用题。1、某厂一车间上半年生产零件48万件,是下半年产量的
 ,该车间全年的产量是多少?
,该车间全年的产量是多少?2、高铁列车的运行速度是380千米/小时,普通列车的速度是它的
 。普通列车的速度是多少?
。普通列车的速度是多少?3、用120cm的铁丝做一个长方体框架。长、宽、高的比是3:2:1。这个长方体的体积是多少?
4、一个圆形花坛。周长是25.12m。如果在这个花坛的周围铺上一条宽1m的环形小路,这条小路的面积是多少平方米?
5、校园里有杨树40棵,是柳树的
 。松树棵数是柳树的
。松树棵数是柳树的 。松树有多少棵?
。松树有多少棵?6、某厂为青海玉树灾区赶制一批帐篷。第一天生产了这批帐篷的
 ,第二天生产了总数的
,第二天生产了总数的 。两天共生产4400顶。第一天生产了多少顶?
。两天共生产4400顶。第一天生产了多少顶?
求阴影部分的面积。(单位:cm)1、外圆半径:5,内圆半径:3
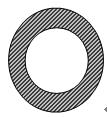
2、d=10(三角形以及直径d下面的部分)

|
解方程。(1)

(2)
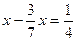
(3)
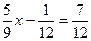
(4)
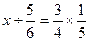
先化简再求值:当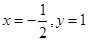 时,求代数式
时,求代数式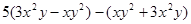 的值。
的值。