如图,已知 , ,抛物线 过 、 两点,并与过 点的直线 交于点 .
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点 ,使四边形 的周长最小?若存在,求出点 的坐标,若不存在,请说明理由;
(3)点 为 轴右侧抛物线上一点,过点 作直线 的垂线,垂足为 .问:是否存在这样的点 ,使以点 、 、 为顶点的三角形与 相似,若存在,求出点 的坐标,若不存在,请说明理由.

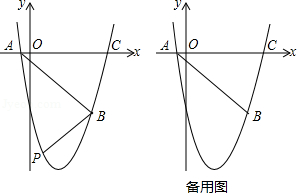
如图,抛物线 (a、b、c为常数, )经过点A(﹣1,0),B(5,﹣6),C(6,0).
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
如图所示,在Rt△ABC与Rt△OCD中, ,O为AB的中点.
(1)求证: .
(2)已知点E在AB上,且 .
(i)若 , ,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.

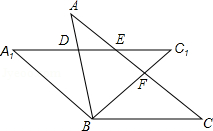
如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
(1)求证: .
(2)当 度时,判定四边形A1BCE的形状并说明理由.
甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, )
