如图,在平面直角坐标系中,抛物线 经过点 和点 ,抛物线 ,动直线 与抛物线 交于点 ,与抛物线 交于点 .
(1)求抛物线 的表达式;
(2)直接用含 的代数式表示线段 的长;
(3)当 是以 为直角边的等腰直角三角形时,求 的值;
(4)在(3)的条件下,设抛物线 与 轴交于点 ,点 在 轴右侧的抛物线 上,连接 交 轴于点 ,连接 ,在平面内有一点 ,连接 和 ,当 且 时,请直接写出点 的坐标.

已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: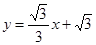 对称.
对称.
(1)求A、B两点坐标,并证明点A在直线l上;
(2)求二次函数解析式;
(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.
如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x﹣2)2+m的x的取值范围.
写出下图中的几何体的名称,找出生活中与下列几何体形状类似的物体各1个.



(1) (2) (3) (4)
如图所示,一个长方体有多少个面?多少条棱?多少个顶点?猜想十棱柱有几个面?几条棱?几个顶点?
图形的识别:说出下图中各图形的名称.(说几何体)