节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求:汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米?
(2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过50元,则至少需要用电行驶多少千米?
如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为0.7米,梯子滑动后停在DE的位置上,测得BD长为1.3米,求梯子顶端A下落了多少米?
如图,M是Rt△ABC斜边AB上的中点,D是边BC延长线上一点,∠B=2∠D,AB=16cm,求线段CD的长.
如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AB=17,BD=12,
(1)求证:△BCD≌△ACE;
(2)求DE的长度.
如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
求证:△ACD≌△BCE.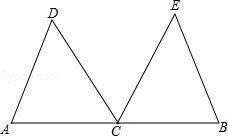
如图,已知:AB=CB,AD=CD,求证:∠A=∠C.