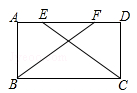
如图,在平面直角坐标系 中,一次函数 与二次函数 的图象相交于 、 两点,点 ,点 为抛物线的顶点.
(1)求二次函数的表达式;
(2)长度为 的线段 在线段 (不包括端点)上滑动,分别过点 、 作 轴的垂线交抛物线于点 、 ,求四边形 面积的最大值;
(3)直线 上是否存在点 ,使得点 关于直线 的对称点 满足 ?若存在,求出点 的坐标;若不存在,请说明理由.

经统计分析.某市跨河大桥上的车流速度v(千米/时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞.此时车流速度为0千米/时;当车流密度不超过20辆/千米,车流速度为80千米/时.研究表明:当 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(1)求大桥上车流密度为100辆/千米时的车流速度;
(2)在某一交通时段.为使大桥上的车流速度大于60千米/时且小于80千米/时,应把大桥上的车流密度控制在什么范围内?
某学校体育看台的侧面如图中阴影部分所示,看台有四级高度相等的小台阶,已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为0.8米的不锈钢架杆AD和8C(杆子的底端分别为D、C),且∠DAB=66.5°(cos66.5°≈0.4).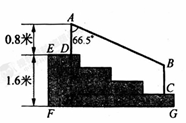
(1)求点D与点C的高度差DH;
(2)求所用不锈钢材料的总长度(即AD+AB+BC的长).
计算: .
.
用4张相同的小纸条做成甲、乙、丙、丁4支签,放在一个盒子中,搅匀后先从盒子中任意抽出1支签(不放回),再从剩余的3支签中任意抽出1支签.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求抽出的两支签中,1支为甲签、1支为丁签的概率.
已知,如图,在矩形ABCD中,点E,F在边AD上,且AE=DF,求证:BF=CE.