一只不透明的袋子中装有4个大小、质地都相同的乒乓球,球面上分别标有数字1、2、3、4.
(1)搅匀后从中任意摸出1个球,求摸出的乒乓球球面上数字为1的概率;
(2)搅匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,求2次摸出的乒乓球球面上数字之和为偶数的概率.
如图,若∠ AOB=30°,点P在∠AOB内,且OP=2㎝,分别在 OA、OB上找一点E,F使△PEF的周长最小,并求△PEF的周长最小值。
AOB=30°,点P在∠AOB内,且OP=2㎝,分别在 OA、OB上找一点E,F使△PEF的周长最小,并求△PEF的周长最小值。
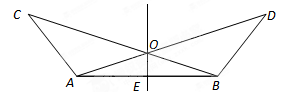
如图所示,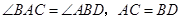 ,点
,点 是
是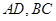 的交点,点
的交点,点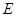 是
是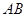 的中点.试判断
的中点.试判断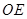 和
和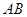 的位置关系,并给出证明
的位置关系,并给出证明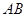
一艘轮船先向正东方向航行2小时,再向西北方向航行 t小 时。船的航速是每小时
25千米。
试用关于 t 的代数式表示船离出发地的距离;
.某食品厂打折出售商品,第一天卖出m千克,第二天比第一天多卖出2千克,第三天卖出的是第一天的3倍,求这个食品厂三天一共卖出食品多少千克?
甲、乙两地间铁路长2400千米, 经技术改造后, 列车实现了提速. 提速后比提速前速度增加20千米/时, 列车从甲地到乙地行驶时间减少4小时. 已知列车在现有条件下安全行驶的速度不超过140千米/时. 请你用学过的数学知识说明这条铁路在现有条件下是否还可以再次提速?