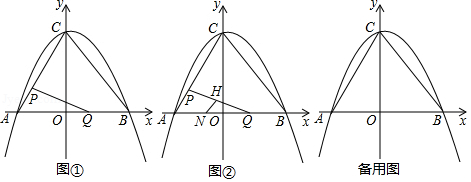
如图①，在平面直角坐标系中，二次函数y13x2bxc的图象与-优题课

解不等式组 $\{\begin{matrix} 4 (x + 1) ⩽ 7 x + 13 \\ x - 4 < \frac{x - 8}{3} \end{matrix}$ ，并写出它的所有负整数解．

计算或化简：

（1） $\sqrt{8} - {(3 - π)}^{0} - 4 \cos 45 °$ ；

（2） $\frac{a^{2}}{a - 1} + \frac{1}{1 - a}$ ．

如图所示，二次函数 $y = k {(x - 1)}^{2} + 2$ 的图象与一次函数 $y = kx - k + 2$ 的图象交于 $A$ 、 $B$ 两点，点 $B$ 在点 $A$ 的右侧，直线 $AB$ 分别与 $x$ 、 $y$ 轴交于 $C$ 、 $D$ 两点，其中 $k < 0$ ．

（1）求 $A$ 、 $B$ 两点的横坐标；

（2）若 $ΔOAB$ 是以 $OA$ 为腰的等腰三角形，求 $k$ 的值；

（3）二次函数图象的对称轴与 $x$ 轴交于点 $E$ ，是否存在实数 $k$ ，使得 $∠ ODC = 2 ∠ BEC$ ，若存在，求出 $k$ 的值；若不存在，说明理由．

（生活观察）甲、乙两人买菜，甲习惯买一定质量的菜，乙习惯买一定金额的菜，两人每次买菜的单价相同，例如：

第一次：

	菜价3元 $/$ 千克
	质量	金额
甲	1千克	3元
乙	1千克	3元

第二次：

	菜价2元 $/$ 千克
	质量	金额
甲	1千克	元
乙	千克	3元

（1）完成上表；

（2）计算甲两次买菜的均价和乙两次买菜的均价．（均价 $=$ 总金额 $\div$ 总质量）

（数学思考）设甲每次买质量为 $m$ 千克的菜，乙每次买金额为 $n$ 元的菜，两次的单价分别是 $a$ 元 $/$ 千克、 $b$ 元 $/$ 千克，用含有 $m$ 、 $n$ 、 $a$ 、 $b$ 的式子，分别表示出甲、乙两次买菜的均价 $\overset{̅}{x_{甲}}$ 、 $\overset{̅}{x_{乙}}$ ，比较 $\overset{̅}{x_{甲}}$ 、 $\overset{̅}{x_{乙}}$ 的大小，并说明理由．

（知识迁移）某船在相距为 $s$ 的甲、乙两码头间往返航行一次．在没有水流时，船的速度为 $v$ ，所需时间为 $t_{1}$ ；如果水流速度为 $p$ 时 $(p < v)$ ，船顺水航行速度为 $(v + p)$ ，逆水航行速度为 $(v - p)$ ，所需时间为 $t_{2}$ ．请借鉴上面的研究经验，比较 $t_{1}$ 、 $t_{2}$ 的大小，并说明理由．

体育器材室有 $A$ 、 $B$ 两种型号的实心球，1只 $A$ 型球与1只 $B$ 型球的质量共7千克，3只 $A$ 型球与1只 $B$ 型球的质量共13千克．

（1）每只 $A$ 型球、 $B$ 型球的质量分别是多少千克？

（2）现有 $A$ 型球、 $B$ 型球的质量共17千克，则 $A$ 型球、 $B$ 型球各有多少只？