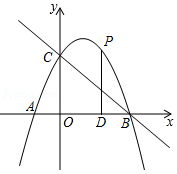
如图,二次函数 的图象与 轴交于 、 两点,与 轴交于点 , .点 在函数图象上, 轴,且 ,直线 是抛物线的对称轴, 是抛物线的顶点.
(1)求 、 的值;
(2)如图①,连接 ,线段 上的点 关于直线 的对称点 恰好在线段 上,求点 的坐标;
(3)如图②,动点 在线段 上,过点 作 轴的垂线分别与 交于点 ,与抛物线交于点 .试问:抛物线上是否存在点 ,使得 与 的面积相等,且线段 的长度最小?如果存在,求出点 的坐标;如果不存在,说明理由.

计算:
已知 ,求 的值.
计算: .
如图,抛物线 与坐标轴交点分别为 , , ,作直线 .
(1)求抛物线的解析式;
(2)点 为抛物线上第一象限内一动点,过点 作 轴于点 ,设点 的横坐标为 ,求 的面积 与 的函数关系式;
(3)条件同(2),若 与 相似,求点 的坐标.
某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况,进行了统计调查.随机调查了某班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类)并将调查结果绘成如下不完整的统计图.根据两图提供的信息,回答下列问题:
(1)最喜欢娱乐类节目的有 人,图中 ;
(2)请补全条形统计图;
(3)根据抽样调查结果,若该校有1800名学生,请你估计该校有多少名学生最喜欢娱乐类节目;
(4)在全班同学中,有甲、乙、丙、丁等同学最喜欢体育类节目,班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲、乙两同学的概率.
