如图,已知正方形 的边长为4,点 是 边上的一个动点,连接 ,过点 作 的垂线交 于点 ,以 为边作正方形 ,顶点 在线段 上,对角线 、 相交于点 .
(1)若 ,则 ;
(2)①求证:点 一定在 的外接圆上;
②当点 从点 运动到点 时,点 也随之运动,求点 经过的路径长;
(3)在点 从点 到点 的运动过程中, 的外接圆的圆心也随之运动,求该圆心到 边的距离的最大值.

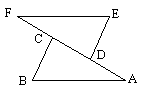
如图所示,已知BD⊥CD于D,EF⊥CD于F, ,
, ,其中
,其中 为锐角,求证:
为锐角,求证: 。
。
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2),过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N。
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数 (x>0)的图象与△MNB有公共点,请直接写出m的取值范围。
(x>0)的图象与△MNB有公共点,请直接写出m的取值范围。
如图, 是半径为
是半径为 的
的 上的定点,动点
上的定点,动点 从
从 出发,以
出发,以 的速度沿圆周逆时针运动,当点
的速度沿圆周逆时针运动,当点 回到
回到 地立即停止运动.
地立即停止运动.
(1)如果 ,求点
,求点 运动的时间;
运动的时间;
(2)如果点 是
是 延长线上的一点,
延长线上的一点, ,那么当点
,那么当点 运动的时间为
运动的时间为 时,判断直线
时,判断直线 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.
如图,E是矩形ABCE的边BC上一点,EF⊥AE,EF分别交AC、CD于点M、F,BG⊥AC,垂足为G,BG交AE于点H。
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=2,求EM的长。
如图所示,已知△ABC≌△FED,且BC=ED,那么AB与EF平行吗?为什么?