为迎接“国家卫生城市”复检,某市环卫局准备购买 、 两种型号的垃圾箱,通过市场调研得知:购买3个 型垃圾箱和2个 型垃圾箱共需540元;购买2个 型垃圾箱比购买3个 型垃圾箱少用160元.
(1)每个 型垃圾箱和 型垃圾箱各多少元?
(2)现需要购买 , 两种型号的垃圾箱共300个,分别由甲、乙两人进行安装,要求在12天内完成(两人同时进行安装).已知甲负责 型垃圾箱的安装,每天可以安装15个,乙负责 型垃圾箱的安装,每天可以安装20个,生产厂家表示若购买 型垃圾箱不少于150个时,该型号的产品可以打九折;若购买 型垃圾箱超过150个时,该型号的产品可以打八折,若既能在规定时间内完成任务,费用又最低,应购买 型和 型垃圾箱各多少个?最低费用是多少元?
(本题5分)有理数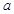 、
、 、
、 在数轴上的位置如图
在数轴上的位置如图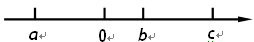
(1)判断正负,用“>”或“<”填空: c-b__0,a-b__0,a+c__0
(2)化简: |c-b|+|a-b|-|a+c|
已知:A=2a2+3ab-2a-1,B=-a2+ab-1 (1)(本题3分)求3A+6B.
(2) (本题2分)若3A+6B的值与a的取值无关,求b的值.
化简(每题4分,共20分)(1) 3x2+2x-5x2+3x
(2) 4(m2+n)+2(n-2m2)
(3) -3(2x2-xy)-(x2+xy-6)
(4) -(6a3b+2b2)+(4a3b-8b2)
(5)先化简,再求值:3x2y-[2x2y-(2xy-3x2y)]+3xy2,其中x=3,y=-
计算(每题3分,共15分)(1) -9+12-3+8
(2) (-1)+(-)+(+)-(+)
(3) (-3)÷2÷(-3)×(-0.75)
(4) -16-(1-0.5)××[2-(-3)2]
(5)用简便方法计算 (-12
计算:
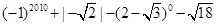 .
.