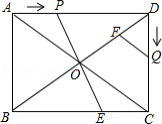
已知:如图,在矩形 中, , ,对角线 , 交于点 .点 从点 出发,沿 方向匀速运动,速度为 ;同时,点 从点 出发,沿 方向匀速运动,速度为 ;当一个点停止运动时,另一个点也停止运动.连接 并延长,交 于点 ,过点 作 ,交 于点 .设运动时间为 ,解答下列问题:
(1)当 为何值时, 是等腰三角形?
(2)设五边形 的面积为 ,试确定 与 的函数关系式;
(3)在运动过程中,是否存在某一时刻 ,使 ?若存在,求出 的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻 ,使 平分 ?若存在,求出 的值;若不存在,请说明理由.
计算
(1)
(2) -
-
如图所示,已知AB∥CD,AB=CD,BF=CE,求证:AE=DF.
如图所示,已知△ABC两内角的平分线AO、BO相交于点O,若∠AOB=140°,求∠C的度数.
如图,有分别过A、B两个加油站的公路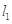 、
、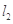 相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且P到两条公路
相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且P到两条公路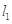 、
、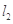 的距离也相等.请用尺规作图作出点P(不写作法,保留作图痕迹)
的距离也相等.请用尺规作图作出点P(不写作法,保留作图痕迹)
某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支.
(1)求第一次每支铅笔的进价是多少元?
(2)若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?