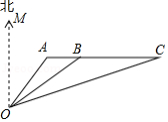
如图,码头 、 分别在海岛 的北偏东 和北偏东 方向上,仓库 在海岛 的北偏东 方向上,码头 、 均在仓库 的正西方向,码头 和仓库 的距离 ,若将一批物资从仓库 用汽车运送到 、 两个码头中的一处,再用货船运送到海岛 ,若汽车的行驶速度为 ,货船航行的速度为 ,问这批物资在哪个码头装船,最早运抵海岛 ?(两个码头物资装船所用的时间相同,参考数据: ,
如图,已知一次函数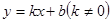 的图像与
的图像与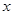 轴,
轴,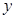 轴分别交于A(1,0)、B(0,-1)两点,且又与反比例函数
轴分别交于A(1,0)、B(0,-1)两点,且又与反比例函数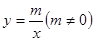 的图像在第一象限交于C点,C点的横坐标为2.
的图像在第一象限交于C点,C点的横坐标为2.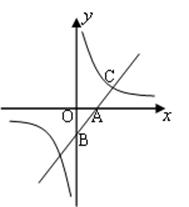
求一次函数的解析式;
求C点坐标及反比例函数的解析式
如图,在直角三角形ABC中,∠ACB=90°,AC=BC=10,将△ABC绕点B沿顺时针方向旋转90°得到△A1BC1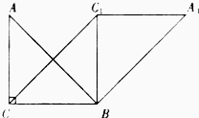
线段A1C1的长度是 ,∠CBA1的度数是 .
连接CC1,求证:四边形CBA1C1是平行四边形.
某市为争创全国文明卫生城,2008年市政府对市区绿化工程投入的资金是2000万元,2010年投入的资金是2420万元,且从2008年到2010年,两年间每年投入资金的年平均增长率相同.求该市对市区绿化工程投入资金的年平均增长率
若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?
已知,如图E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE,四边形ABCD是平行四边形吗?请说明理由.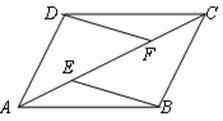
某中学为了了解学生的体育锻炼情况,随机抽查了部分学生一周参加体育锻炼的时间,得到如图的条形统计图,根据图形解答下列问题:
这次抽查了 名学生
所抽查的学生一周平均参加体育锻炼多少小时?
已知该校有1200名学生,估计该校有多少名学生一周参加体育锻炼的时间超过6小时?