某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。求:
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E。求证:点E为AD的中点
关于 的一元二次方程
的一元二次方程
(1)求证:方程有两个不相等的实数根;
(2)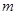 为何整数时,此方程的两个根都为正整数.
为何整数时,此方程的两个根都为正整数.
解一元二次方程.
(1)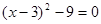
(2)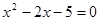
(3)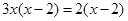
(4)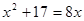
如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.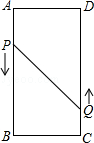
(1)若点P从点A移动到点B停止,点P、Q分别从点A、C同时出发,问经过2s时P、Q两点之间的距离是多少cm?
(2)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(3)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?