铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀．小张购进一批食材制作特色美食，每盒售价为50元，由于食材需要冷藏保存，导致成本逐日增加，第 天 且 为整数）时每盒成本为 元，已知 与 之间满足一次函数关系；第3天时，每盒成本为21元；第7天时，每盒成本为25元，每天的销售量为 盒， 与 之间的关系如下表所示：
第 天 |
|
|
每天的销售量 盒 |
10 |
|
（1）求 与 的函数关系式；
（2）若每天的销售利润为 元，求 与 的函数关系式，并求出第几天时当天的销售利润最大，最大销售利润是多少元？
（3）在“荷花美食”厨艺秀期间，共有多少天小张每天的销售利润不低于325元？请直接写出结果．
求代数式的值：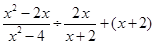
，其中
.
解不等式: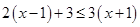
.
计算：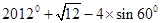
已知在平面直角坐标系中，直线与x轴，y轴相交于A,B两点，
直线与AB相交于C点，点D从点O出发，以每秒1个单位的速度沿x轴向右运
动到点A，过点D作x轴的垂线，分别交直线和直线于P,Q两点（P点不与C点重合），以PQ为边向左作正△PQR，设正△PQR与△OBC重叠部分的面积为S（平方单位），点D的运动时间为t（秒）
（1）求点A,B,C的坐标； （2）若点正好在△PQR的某边上，求t的值；
（3）求S关于t的函数关系式，并写出相应t的取值范围，
求出D在整个运动过程中s的最大值。
如图点A点B是反比例函数上两点，过这两点的直线 ，且AC∥X轴，AC⊥BC于点C，
①求阴影部分面积（用k的代数式表示）；
②若BC和AC分别交x轴、y轴于D,E，连接DE，求证△ABC～ △EDC；
③若求出这两个函数解析式。