如图,抛物线 与 轴的两个交点分别为 , ,与 轴交于点 ,点 在 轴正半轴上,且 .
(1)求抛物线的解析式;
(2)如图1,抛物线的顶点为点 ,对称轴交 轴于点 ,连接 , ,请在抛物线的对称轴上找一点 ,使 ,求出点 的坐标;
(3)如图2,过点 作 轴,交抛物线于点 ,连接 ,点 是 轴上一点,在抛物线上是否存在点 ,使以点 , , , 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.

张大伯计划建一个面积为72平方米的矩形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙长15米),另外的部分(包括中间的隔墙)用30米的竹篱笆围成,如图.
(1)请你通过计算帮助张大伯设计出围养鸡场的方案.
(2)在上述条件不变的情况下,能围出比72平方米更大的养鸡场吗?请说明理由.
先阅读,后解答: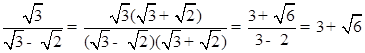
像上述解题过程中,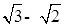 与
与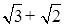 相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)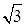 的有理化因式是 ;
的有理化因式是 ; 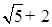 的有理化因式是 .
的有理化因式是 .
(2)将下列式子进行分母有理化:
(1)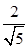 = ;(2)
= ;(2)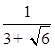 = .
= .
(3)已知a=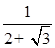 ,b=
,b=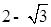 ,比较a与b的大小关系.
,比较a与b的大小关系.
若x=0是关于x的一元二次方程(m﹣2)x2+3x+m2+2m﹣8=0的一个解,求实数m的值和另一个根.
一布袋中有红、黄、白三种颜色的球各一个,它们除颜色外,其它都一样,小亮从布袋摸出一个球后放回去摇匀,再摸出一个球,请你用列举法(列表法或树形图)分析并求出小亮两次都能摸到白球的概率.
解方程:(x+3)2=2(x+7)