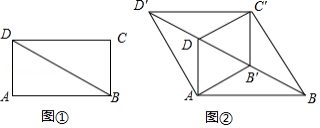
如图,在平面直角坐标系 中,抛物线 与 轴相交于点 ,点 与点 关于点 对称
(1)填空:点 的坐标是 ;
(2)过点 的直线 (其中 与 轴相交于点 ,过点 作直线 平行于 轴, 是直线 上一点,且 ,求线段 的长(用含 的式子表示),并判断点 是否在抛物线上,说明理由;
(3)在(2)的条件下,若点 关于直线 的对称点 恰好落在该抛物线的对称轴上,求此时点 的坐标.
剪纸是中国传统的民间艺术,它画面精美,风格独特,深受大家喜爱,现有三张不透明的卡片,其中两张卡片的正面图案为“金鱼”,另外一张卡片的正面图案为“蝴蝶”,卡片除正面剪纸图案不同外,其余均相同.将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求抽出的两张卡片上的图案都是“金鱼”的概率.(图案为“金鱼”的两张卡片分别记为 、 ,图案为“蝴蝶”的卡片记为

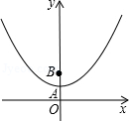
《函数的图象与性质》拓展学习片段展示:
【问题】如图①,在平面直角坐标系中,抛物线 经过原点 ,与 轴的另一个交点为 ,则 .
【操作】将图①中抛物线在 轴下方的部分沿 轴折叠到 轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为 ,如图②.直接写出图象 对应的函数解析式.
【探究】在图②中,过点 作直线 平行于 轴,与图象 的交点从左至右依次为点 , , , ,如图③.求图象 在直线 上方的部分对应的函数 随 增大而增大时 的取值范围.
【应用】 是图③中图象 上一点,其横坐标为 ,连接 , .直接写出 的面积不小于1时 的取值范围.
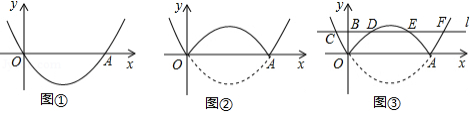
如图,在 中, , , .点 从点 出发,以 的速度沿边 向终点 运动.过点 作 交折线 于点 , 为 中点,以 为边向右侧作正方形 .设正方形 与 重叠部分图形的面积是 ,点 的运动时间为 .
(1)当点 在边 上时,正方形 的边长为 (用含 的代数式表示);
(2)当点 不与点 重合时,求点 落在边 上时 的值;
(3)当 时,求 关于 的函数解析式;
(4)直接写出边 的中点落在正方形 内部时 的取值范围.
如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水, 时注满水槽.水槽内水面的高度 与注水时间 之间的函数图象如图②所示.
(1)正方体的棱长为 ;
(2)求线段 对应的函数解析式,并写出自变量 的取值范围;
(3)如果将正方体铁块取出,又经过 恰好将此水槽注满,直接写出 的值.

如图①, 是矩形 的对角线, , .将 沿射线 方向平移到△ 的位置,使 为 中点,连接 , , , ,如图②.
(1)求证:四边形 是菱形;
(2)四边形 的周长为 ;
(3)将四边形 沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.