如图, 内接于 , 是 的直径,点 是 上的定点, 平分 交 于点 , ,交 延长线于点 .
(1)求证: 与 相切;
(2)作 于点 , 于点 ,试判断线段 、 、 三者之间的数量关系,并证明你的结论(不用尺规作图的方法补全图形).

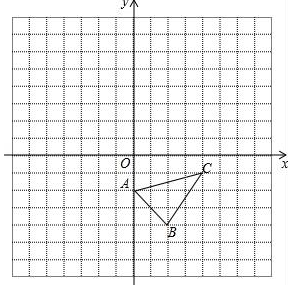
如图,已知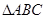 ,
,
(1)画出与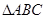 关于
关于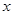 轴对称的图形
轴对称的图形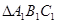 ;
;
(2)写出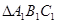 各顶点坐标.
各顶点坐标.
解方程: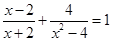
如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
(1)点A的坐标是 ,n= ,k= ,b= ;
(2)x取何值时,函数y=kx+b的函数值大于函数y=x+1的函数值;
(3)求四边形AOCD的面积;
(4)是否存在y轴上的点P,使得以点P,B,D为顶点的三角形是等腰三角形?若存在求出点P的坐标;若不存在,请说明理由.
如图1,将射线OX按逆时针方向旋转β角,得到射线OY,如果点P为射线OY上的一点,且OP=a,那么我们规定用(a,β)表示点P在平面内的位置,并记为P(a,β),例如,图2中,如果OM=8,∠XOM=110°,那么点M在平面内的位置,记为M(8,110),根据图形,解答下面的问题:
(1)如图3,如果点N在平面内的位置记为N(6,30),那么ON= ;∠XON= .
(2)如果点A、B在平面内的位置分别记为A(5,30),B(12,120),试求A、B两点之间的距离并画出图.
某气象研究中心观测一场沙尘暴从发生到结束全过程,开始时风暴平均每小时增加2千米/时,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米/时,一段时间,风暴保持不变,当沙尘暴遇到绿色植被区时,其风速平均每小时减小1千米/时,最终停止.结合风速与时间的图象,回答下列问题:
(1)在y轴()内填入相应的数值;
(2)沙尘暴从发生到结束,共经过多少小时?
(3)求出当x≥25时,风速y(千米/时)与时间x(小时)之间的函数关系式;
(4)若风速达到或超过20千米/时,称为强沙尘暴,则强沙尘暴持续多长时间?