某学习小组的学生在学习中遇到了下面的问题:
如图1,在
和
中,
,
,点
,
,
在同一条直线上,连接
,点
是
的中点,连接
,
,试判断
的形状并说明理由.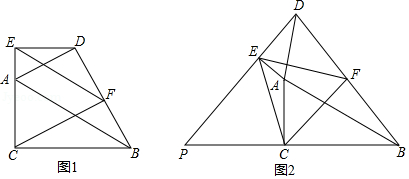
问题探究:
(1)小婷同学提出解题思路:先探究 的两条边是否相等,如 ,以下是她的证明过程
证明:延长线段 交 的延长线于点 . 是 的中点, . , . |
. 又 , . . . |
请根据以上证明过程,解答下列两个问题:
①在图1中作出证明中所描述的辅助线;
②在证明的括号中填写理由(请在 , , , 中选择).
(2)在(1)的探究结论的基础上,请你帮助小婷求出 的度数,并判断 的形状.
问题拓展:
(3)如图2,当 绕点 逆时针旋转某个角度时,连接 ,延长 交 的延长线于点 ,其他条件不变,判断 的形状并给出证明.
图甲是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块全等的小长方形,然后按图乙的形状拼成一个正方形.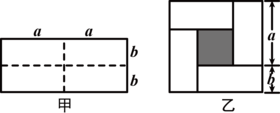
(1)图乙的阴影部分的正方形的边长是;
(2)用两种不同的方法求图乙中阴影部分的面积.
【方法1】 S阴影=;
【方法2】 S阴影=;
(3)观察图27.2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系;
(4)根据(3)题中的等量关系,解决问题:若x+y=10,xy=16,求x-y的值.
如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°,设p=BC+CD, 四边形ABCD的面积为S.
(1)试探究 与
与 之间的关系,并说明理由;
之间的关系,并说明理由;
(2)若四边形 的面积为9,求
的面积为9,求 的值.
的值.
如图.等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.

(1)试判定△ODE的形状.并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.
已知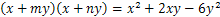 ,求
,求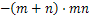 的值.
的值.
先化简,再求值: 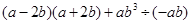 ,其中
,其中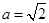 ,
,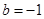 .
.