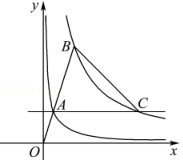
如图,分别位于反比例函数 , 在第一象限图象上的两点 、 ,与原点 在同一直线上,且 .
(1)求反比例函数 的表达式;
(2)过点 作 轴的平行线交 的图象于点 ,连接 ,求 的面积.
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.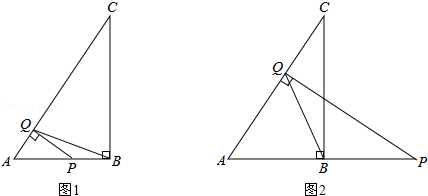
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
在一次课外活动中,李聪、何花、王军三位同学准备跳绳,他们约定用“抛硬币”的游戏方式来确定哪两位同学先用绳(如图1).
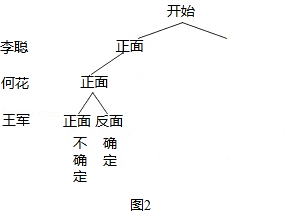
(1)请将如图2表示游戏一个回合所有可能出现结果的树状图补充完整;
(2)求一个回合能确定两位同学先用绳的概率.
已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
如图所示,一艘渔船正以30海里/时的速度由西向东追赶鱼群,自A处经半小时到达B处,在A处看见小岛C在船的北偏东60°的方向上,在B处看见小岛C在船的北偏东30°的方向上,已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,则这艘船继续向东追赶鱼群,是否有进入危险区域的可能?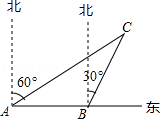
已知在△ABC中,∠BAC=90°;分别以AB,BC为边作正方形ABDE和正方形BCFG,连接DC,GA交于点P,求证:PD⊥PG.