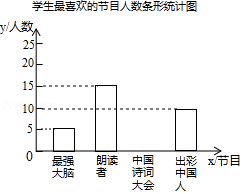
为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
学生最喜爱的节目人数统计表
节目 |
人数(名 |
百分比 |
最强大脑 |
5 |
|
朗读者 |
15 |
|
中国诗词大会 |
|
|
出彩中国人 |
10 |
|
根据以上提供的信息,解答下列问题:
(1) , , ;
(2)补全上面的条形统计图;
(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
已知a、b、c满足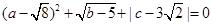 .
.
(1)求a、b、c的值;
(2)试问以a、b、c为边长能否构成三角形?若能构成,求出三角形周长;若不能构成三角形,请说明理由.
阅读解题过程,请判断解答是否正确.若不正确,写出正确的解答过程.
已知a为实数,化简: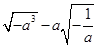 .
.
解: .
.
已知长方形的长为 ,宽为
,宽为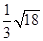 .
.
(1)求长方形的周长;
(2)求与长方形面积相等的正方形的周长,并比较正方形周长与长方形周长的大小;
(3)通过计算,你从中得到了什么启示?
如图所示,已知正方形ABCD的面积是49cm2,正方形EFGH的面积是25cm2,且AH=DG=CF=BE,求AD、EF的长及△AEH的面积.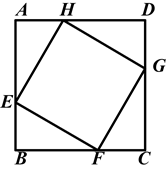
在一块边长为 m的正方形土地中,修建了一个边长为
m的正方形土地中,修建了一个边长为 m的正方形养鱼池,问:剩余部分的面积是多少?
m的正方形养鱼池,问:剩余部分的面积是多少?