为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩用如图的折线统计图表示:(甲为实线,乙为虚线)
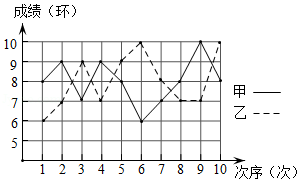
(1)依据折线统计图,得到下面的表格:
射击次序(次 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
甲的成绩(环 |
8 |
9 |
7 |
9 |
8 |
6 |
7 |
|
10 |
8 |
乙的成绩(环 |
6 |
7 |
9 |
7 |
9 |
10 |
8 |
7 |
|
10 |
其中 , ;
(2)甲成绩的众数是 环,乙成绩的中位数是 环;
(3)请运用方差的知识,判断甲、乙两人谁的成绩更为稳定?
(4)该校射击队要参加市组织的射击比赛,已预选出2名男同学和2名女同学,现要从这4名同学中任意选取2名同学参加比赛,请用列表或画树状图法,求出恰好选到1男1女的概率.
一位在读大学生利用假期去一家公司打工,报酬按每时15元计算.设该生打工时间为t时,应得报酬为w元.
| 工作时间t(时) |
2 |
5 |
10 |
… |
t |
| 报酬w(元) |
… |
(1)填表:
(2)用t表示w;
(3)指出哪些是常量,哪些是变量.
如图,把一个“瘦长”的圆柱(圆钢条)锻压成一个“矮胖”的圆柱.
(1)在这个变化过程中,考察圆柱的体积、表面积、侧面积、半径、高,指出哪些是变量;
(2)你能求出高h关于半径r的关系式吗?并说出r、h的变化趋势.
行驶中的汽车,在刹车后由于惯性的作用,还将继续向前滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号汽车的刹车性能(车速不超过140千米/时),对这种汽车进行测试,测得数据如下表:
| 刹车时车速(千米/时) |
20 |
40 |
60 |
80 |
100 |
120 |
| 刹车距离(米) |
1.0 |
3.6 |
7.8 |
13.6 |
21 |
30 |
回答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量,哪个是因变量?
(2)如果刹车时车速为60千米/时,那么刹车距离是多少米?
林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,这里什么是变量,什么是常量?
说出下列各个过程中的变量与常量:
(1)我国第一颗人造地球卫星绕地球一周需106分钟,t分钟内卫星绕地球的周数为N,N= ;
;
(2)铁的质量m(g)与体积V(cm3)之间有关系式;
(3)矩形的长为2cm,它的面积为S(m2)与宽a(cm)的关系式是S=2a.