如图,在平面直角坐标系中,二次函数 交 轴于点 、 ,交 轴于点 ,在 轴上有一点 ,连接 .
(1)求二次函数的表达式;
(2)若点 为抛物线在 轴负半轴上方的一个动点,求 面积的最大值;
(3)抛物线对称轴上是否存在点 ,使 为等腰三角形?若存在,请直接写出所有 点的坐标,若不存在,请说明理由.

用计算器求下列各式的值:
(1)sin20°; (2)cos38°;(3)tan10°;(4)tan80°;
(5)cos27°51′;(6)tan56°17′35″; (7)sin75°31′12″; (8)3sin29°.
如图,点A的坐标是(0.5,0),现在点A绕着点O按逆时针方向旋转, 每秒钟旋转30°,同时点A离开O点的距离以每秒0.5个单位的速度在增大,当A点第11 秒钟时到达图中的P点处,求P点的坐标.

某学生站在公园湖边的M处,测得湖心亭A位于北偏东30°方向上,又测得游船码头B位于南偏东60°方向上.现有一艘游船从湖心亭A 处沿正南方向航行返回游船码头,已知M处与AB的距离MN=0.7千米,求湖心亭与游船码头B的距离(精确到0.1千米).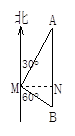
要求tan30°的值,可构造如图所示的直角三角形进行计算.
作Rt△ABC,使∠C=90°,斜边AB=2,直角边AC=1,那么BC= ,∠ABC=" 30" °
,∠ABC=" 30" °
∴tan30°= .
.
在此图的基础上,通过添加适当的辅助线,可求出tan15°的值,请简要写出你添加的辅助线和求出的tan15°的值.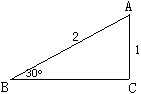
如图,有一个同学用一个含有30°角的直角三角板估测他们学校的旗杆AB 的高度,他将30°的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为15米,求旗杆AB的高度(精确到0.1米).