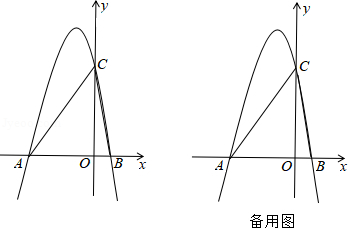
如图,已知抛物线 与 轴交于点 和点 ,与 轴交于点 .
(1)求抛物线 的函数表达式及点 的坐标;
(2)点 为坐标平面内一点,若 ,求点 的坐标;
(3)在抛物线上是否存在点 ,使 ?若存在,求出满足条件的所有点 的坐标;若不存在,请说明理由.
如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线 上的点,且△ACE是等边三角形.
上的点,且△ACE是等边三角形.
(1)试说明:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,试说明:四边形ABCD是正方形
某 校八年级(1)班48名学生参加2010年该市数学期中考试,全班学生的成绩统计如下表:
校八年级(1)班48名学生参加2010年该市数学期中考试,全班学生的成绩统计如下表:
| 成绩(分) |
72 |
75 |
78 |
80 |
82 |
83 |
85 |
86 |
88 |
90 |
91 |
92 |
95 |
| 人数(人) |
2 |
1 |
3 |
4 |
4 |
3 |
7 |
4 |
6 |
4 |
3 |
5 |
2 |
请根据表中提供的信息解答下列问题:
(1)该班学生考试成绩的平均分是分(精确到0.01);
(2)众数是分,中位数是分;
(3)该班小明同学在这次考试中的成绩是82分,说说小明同学的成绩处于全班中上还是中下水平?为什么?
计算:(本题每小题4分,满分8分)
(1)求右式中x的值:4(x+1 =64
=64
(2)
已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为x.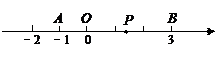
(1)若点P到点A、点B的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为6?若存在,请求出x的值;若不存在,说明理由.
(3)点A、点B分别以2个单位长度/分、1个单位长度/分的速度向右运动,同时点P以6个单位长度/分的速度从O点向左运动.当遇到A时,点P立即以同样的速度向右运动,并不停地往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?
学校植物园沿路护栏纹饰部分设计成若干个相同的菱形图案,每增加一个菱形图案,纹饰长度就增加d cm,如图所示.已知每个菱形的横向对角线长为30cm.
(1)若该纹饰要231个菱形图案,试用含d的代数式表示纹饰的长度L;
当d=26时,求该纹饰的长度L;
(2)当d=20时,若保持(1)中纹饰长度不变,则需要多少个这样的菱形图案?