如图，已知二次函数yax2bxc的图象与x轴分别交于A、B两-优题课

题文

如图，已知二次函数 $y = a x^{2} + bx + c$ 的图象与 $x$ 轴分别交于 $A$ 、 $B$ 两点，与 $y$ 轴交于 $C$ 点， $OA = OC$ ．则由抛物线的特征写出如下结论：

① $abc > 0$ ；② $4 ac - b^{2} > 0$ ；③ $a - b + c > 0$ ；④ $ac + b + 1 = 0$ ．

其中正确的个数是 $($ 　　 $)$

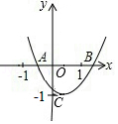
A．4个B．3个C．2个D．1个

科目数学题型选择题难度中等

知识点：二次函数图象与系数的关系抛物线与x轴的交点

相关试题

下图是由几个相同的小正方体搭成的一个几何体，它的俯视图是（）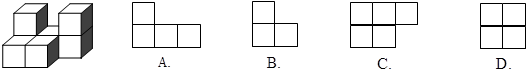

“十二五”期间，我国将新建保障性住房36 000 000套，用于解决中低收入人群和新参加工作的大学生住房的需求，将36 000 000用科学记数法表示应是（）

⁶

如图为二次函数y＝ax²＋bx＋c的图象，在下列说法中：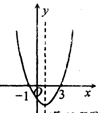

①ac<0；　　　　　 ②2a＋b＝0；
　 ③a＋b＋c>0；　④当x>0.5时，y随x的增大而增大；
　 ⑤对于任意x均有ax²＋ax≥a＋b，
　正确的说法有

如图，以AB为直径的⊙O与AD、DC、BC均相切，若AB＝BC＝4，则OD的长度为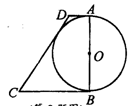

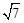A． B． C． D．2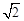

如图，将一个Rt△ABC形状的楔子从木桩的底端点P沿水平方向打入木桩底下，使木桩向上运动．已知楔子斜面的倾斜角为15°，若楔子沿水平方向前进6cm(如箭头所示)，则木桩上升