在一条笔直的公路上依次有 , , 三地,甲、乙两人同时出发,甲从 地骑自行车去 地,途经 地休息1分钟,继续按原速骑行至 地,甲到达 地后,立即按原路原速返回 地;乙步行从 地前往 地.甲、乙两人距 地的路程 (米 与时间 (分 之间的函数关系如图所示,请结合图象解答下列问题:

(1)请写出甲的骑行速度为 米 分,点 的坐标为 ;
(2)求甲返回时距 地的路程 与时间 之间的函数关系式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回 地之前,经过多长时间两人距 地的路程相等.
(本小题满分5分)
已知二次函数 .
.
(1)将 化成y=a (x-h) 2 +k的形式;
化成y=a (x-h) 2 +k的形式;
(2)指出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y随x的增大而增大?
(本小题满分5分)
已知:如图,在 中,D是AC上一点,联结BD,且∠ABD =∠ACB.
中,D是AC上一点,联结BD,且∠ABD =∠ACB.
(1)求证:△ABD∽△ACB;
(2)若AD=5,AB= 7,求AC的长.
如,已知抛物线y = ax2+bx+ c经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),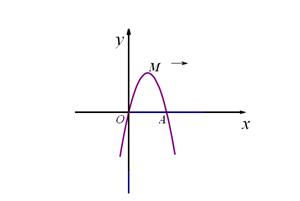
(1)求该抛物线的解析式;
(2)现将它向右平移m(m>0)个单位,所得抛物线与x轴交于C、D两点,与原抛物线交于点P,△CDP的面积为S,求S关于m的关系式;
(3)如图,以点A为圆心,以线段OA为半径画圆交抛物线y = ax2+bx+ c的对称轴于点B,连结AB,
若将抛物线向右平移m(m>0)个单位后,B点的对应点为B′,A点的对应点为A′点,且满足四边形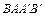 为菱形,平移后的抛物线的对称轴与菱形的对角线BA′交于点E,在x轴上是否存在一点F,
为菱形,平移后的抛物线的对称轴与菱形的对角线BA′交于点E,在x轴上是否存在一点F,
使得以E、F、A′为顶点的三角形与△BAE相似,若存在求出F点坐标,若不存在说明理由. 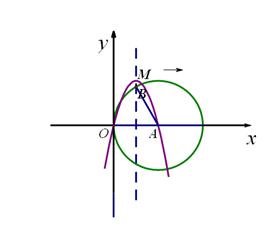
如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即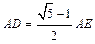 ,BE交DC于点F,已知
,BE交DC于点F,已知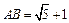 ,求CF的长 .
,求CF的长 .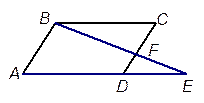
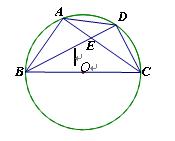
如图,⊙O是△ABC的外接圆,BC是⊙O的直径,
|
D是劣弧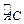 中点,BD交AC于点E.
中点,BD交AC于点E.