某校举办“打造平安校园”活动,随机抽取了部分学生进行校园安全知识测试.将这些学生的测试结果分为四个等级: 级:优秀; 级:良好; 级:及格; 级:不及格,并将测试结果绘制成如下统计图.请你根据图中信息,解答下列问题:
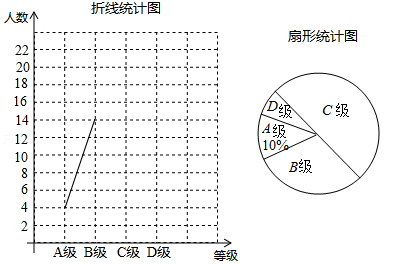
(1)本次参加校园安全知识测试的学生有多少人?
(2)计算 级所在扇形圆心角的度数,并补全折线统计图;
(3)若该校有学生1000名,请根据测试结果,估计该校达到及格和及格以上的学生共有多少人?
甲同学口袋中有三张卡片,分别写着数字1,1,2,乙同学口袋中也有三张卡片,分别写着数字1,2,2.两人各自从自己的口袋中随机摸出一张卡片,若两人摸出的卡片上的数字之和为偶数,则甲胜;否则乙胜.求甲胜的概率.
如图,M是⊙O中弦CD的中点,EM经过点O,若CD="4," EM=6,求⊙O的半径.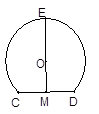
根据下图,化简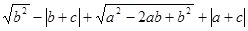

计算: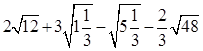
今年春季,我省云南、贵州等西南地区遇到多年不遇旱灾,“一方有难,八方支援”,为及时灌溉农田,丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)及配套相同型号抽水机4台、3台、2台,每台抽水机每小时可抽水灌溉农田1亩。现要求所有柴油发电机及配套抽水机同时工作一小时,灌溉农田32亩。
(1)设甲种柴油发电机的数量为x台,乙种柴油发电机数量y台。
①用含x、y的式子表示丙种柴油发电机的数量;
②求出y与x的函数解析式;
(2)已知甲、乙、丙柴油发电机每小时费用分别为130元、120元 、100元,应如何安排三种柴油发电机的数量,既能按要求抽水灌溉,同时柴油发电机总费用w最少?