探究:小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点 , , , ,可通过构造直角三角形利用图1得到结论: 他还利用图2证明了线段 的中点 的坐标公式: , .

(1)请你帮小明写出中点坐标公式的证明过程;
运用:(2)①已知点 , ,则线段 长度为 ;
②直接写出以点 , , , 为顶点的平行四边形顶点 的坐标: ;
拓展:(3)如图3,点 在函数 的图象 与 轴正半轴夹角的平分线上,请在 、 轴上分别找出点 、 ,使 的周长最小,简要叙述作图方法,并求出周长的最小值.
如图,世博园段的浦江两岸互相平行,C、D是浦西江边间隔200m的两个场馆.海宝在浦东江边的宝钢大舞台 处,测得
处,测得 ,然后沿江边走了500m到达世博文化中心
,然后沿江边走了500m到达世博文化中心 处,测得
处,测得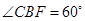 ,求世博园段黄浦江的宽度(结果可保留根号).
,求世博园段黄浦江的宽度(结果可保留根号).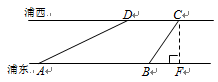
如图,已知 是⊙
是⊙ 的直径,⊙
的直径,⊙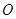 过
过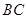 的中点
的中点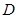 ,且
,且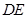 ⊥
⊥ ,垂足为点
,垂足为点 .
.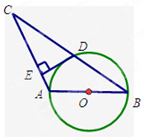
求证:
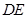 是⊙
是⊙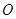 的切线;
的切线;若∠
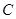 =
=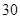 °,
°,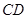 =10cm,求⊙
=10cm,求⊙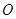 的半径.
的半径.
一只口袋中放着若干只红球和白球,这两种球除了颜色以外没有任何其他区别,袋中的球已经搅匀,蒙上眼睛从口袋中取出一只球,取出红球的概率是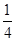 .
.取出白球的概率是多少?
如果袋中的白球有18只,那么袋中的红球有多少只?
已知反比例函数 的图象与一次函数
的图象与一次函数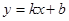 的图象交于点
的图象交于点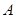 (
(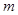 ,2),点
,2),点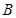 (-2,
(-2, 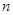 ),一次函数图象与
),一次函数图象与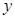 轴的交点为
轴的交点为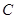 .
.求一次函数解析式;
求
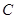 点的坐标;
点的坐标;求△
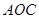 的面积.
的面积.
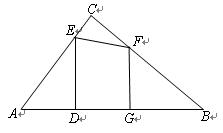
如图,在Rt△ABC中,∠ACB=90º,AB=10,AC=6 ,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.(1)当AD=3时,求DE的长;
(2)当点
 E、F在边AC、BC上移动时,设
E、F在边AC、BC上移动时,设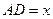 ,
, ,
,
求 关于
关于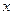 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;(3)在点E、F移动过
 程中,△AED与△CEF能否相似,
程中,△AED与△CEF能否相似,
若能,求AD的长;若不能,请说明理由.