如图,已知抛物线 与 轴相交于点 ,与 正半轴相交于点 ,对称轴是直线
(1)求此抛物线的解析式以及点 的坐标.
(2)动点 从点 出发,以每秒2个单位长度的速度沿 轴正方向运动,同时动点 从点 出发,以每秒3个单位长度的速度沿 轴正方向运动,当 点到达 点时, 、 同时停止运动.过动点 作 轴的垂线交线段 于点 ,交抛物线于点 ,设运动的时间为 秒.
①当 为何值时,四边形 为矩形.
②当 时, 能否为等腰三角形?若能,求出 的值;若不能,请说明理由.
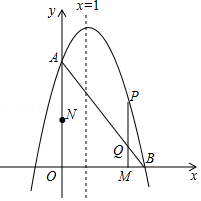
已知二次函数 的图象如图所示,下列说法错误的是()
的图象如图所示,下列说法错误的是()
| A.图象关于直线x=1对称 |
B.函数 的最小值是﹣4 的最小值是﹣4 |
C.方程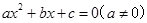 的两个根是﹣1和3 的两个根是﹣1和3 |
| D.当x<1时,y随x的增大而增大 |
在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(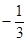 ,
,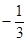 ),(
),(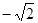 ,
,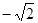 ),…,都是和谐点.
),…,都是和谐点.
(1)分别判断函数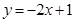 和
和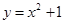 的图象上是否存在和谐点,若存在,求出其和谐点的坐标;
的图象上是否存在和谐点,若存在,求出其和谐点的坐标;
(2)若二次函数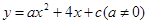 的图象上有且只有一个和谐点(
的图象上有且只有一个和谐点(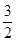 ,
,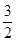 ),且当
),且当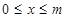 时,函数
时,函数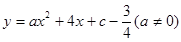 的最小值为-3,最大值为1,求
的最小值为-3,最大值为1,求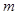 的取值范围;
的取值范围;
(3)直线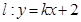 经过和谐点P,与
经过和谐点P,与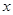 轴交于点D,与反比例函数
轴交于点D,与反比例函数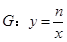 的图象交于M,N两点(点M在点N的左侧),若点P的横坐标为1,且
的图象交于M,N两点(点M在点N的左侧),若点P的横坐标为1,且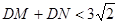 ,请直接写出
,请直接写出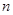 的取值范围.
的取值范围.
△ABC中,∠ABC=45°,AH⊥BC于点H,将△AHC绕点H逆时针旋转90°后,点C的对应点为点D,直线BD与直线AC交于点E,连接EH.
(1)如图1,当∠BAC为锐角时,
①求证:BE⊥AC;
②求∠BEH的度数;
(2)当∠BAC为钝角时,请依题意用实线补全图2,并用等式表示出线段EC,ED,EH之间的数量关系.
抛物线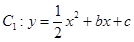 与
与 轴交于点C(0,3),其对称轴与
轴交于点C(0,3),其对称轴与 轴交于点A(2,0).
轴交于点A(2,0).
(1)求抛物线 的解析式;
的解析式;
(2)将抛物线 适当平移,使平移后的抛物线
适当平移,使平移后的抛物线 的顶点为D(0,
的顶点为D(0,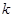 ).已知点B(2,2),若抛物线
).已知点B(2,2),若抛物线 与△OAB的边界总有两个公共点,请结合函数图象,求
与△OAB的边界总有两个公共点,请结合函数图象,求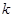 的取值范围.
的取值范围.
阅读下面材料:小军遇到这样一个问题:如图1,△ABC中,AB=6,AC=4,点D为BC的中点,求AD的取值范围.
(1)小军发现老师讲过的“倍长中线法”可以解决这个问题.他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≌△CAD,经过推理和计算使问题得到解决.
请回答:AD的取值范围是.
(2)参考小军思考问题的方法,解决问题:如图3,△ABC中,E为AB中点,P是CA延长线上一点,连接PE并延长交BC于点D.求证:PA•CD=PC•BD.