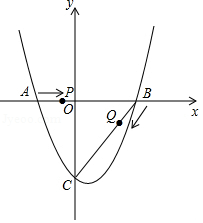
如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点(点 在点 左侧),与 轴交于点 .
(1)求点 , , 的坐标;
(2)点 从 点出发,在线段 上以每秒2个单位长度的速度向 点运动,同时,点 从 点出发,在线段 上以每秒1个单位长度的速度向 点运动,当其中一个点到达终点时,另一个点也停止运动.设运动时间为 秒,求运动时间 为多少秒时, 的面积 最大,并求出其最大面积;
(3)在(2)的条件下,当 面积最大时,在 下方的抛物线上是否存在点 ,使 的面积是 面积的1.6倍?若存在,求点 的坐标;若不存在,请说明理由.
“丰收”种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含l0千克)的种子,超过l0千克的部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.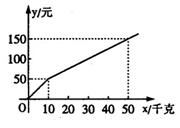
(1)求一次购买种子数量不超过l0千克时的销售价格;
(2)一次购买10千克以上种子时,超过l0千克的那部分种子价格打几折?
(3)一次购买40千克种子比分两次购买且每次购买20千克种子所花的钱少吗?说明理由.
化简: .
.
计算:(2-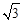 )(2+
)(2+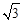 )+
)+
 -
-
解方程
(1)用配方法解方程: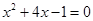 .
.
(2)用公式法解方程: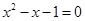
分解因式:
(1)(2a+1)2-(2a+1)(-1+2a)
(2)4(x+y)2-(x-y)2