已知平面图形 ，点 、 是 上任意两点，我们把线段 的长度的最大值称为平面图形 的“宽距”．例如，正方形的宽距等于它的对角线的长度．
（1）写出下列图形的宽距：
①半径为1的圆： ；
②如图1，上方是半径为1的半圆，下方是正方形的三条边的“窗户形“： ；
（2）如图2，在平面直角坐标系中，已知点 、 ， 是坐标平面内的点，连接 、 、 所形成的图形为 ，记 的宽距为 ．
①若 ，用直尺和圆规画出点 所在的区域并求它的面积（所在区域用阴影表示）；
②若点 在 上运动， 的半径为1，圆心 在过点 且与 轴垂直的直线上．对于 上任意点 ，都有 ，直接写出圆心 的横坐标 的取值范围．
某仓库有甲种货物360吨，乙种货物290吨，计划用A、B两种共50辆货车运往外地．已知一辆A种货车的运费需0.5万元，一辆B种货车的运费需0.8万元．
（1）设A种货车为
辆，运输这批货物的总运费为y万元，试写出y与的关系表达式；
（2）若一辆A种货车能装载甲种货物9吨和乙种货物3吨；一辆B种货车能装载甲种货物6吨和乙种货物8吨．按此要求安排A，B两种货车运送这批货物，有哪几种运输方案？请设计出来；
（3）试说明哪种方案总运费最少？最少运费是多少万元？
如图1，在△ABC和△EDC中，AC＝CE＝CB＝CD，∠ACB＝∠ECD＝
，AB与CE交于F，ED与AB、BC分别交于M、H．
图1
(1)求证:CF＝CH；
(2)如图2，△ABC不动，将△EDC绕点C旋转到∠BCE=
时，试判断四边形ACDM是什么四边形？并证明你的结论．
图2
如图，小红同学用仪器测量一棵大树AB的高度，在C处测得∠ADG=30°，在E处测得∠AFG=60°，CE=8米，仪器高度CD=1.5米，求这棵树AB的高度（结果保留两位有效数字，
≈1.732）．
近年来，某县为发展教育事业，加大了对教育经费的投入，2010年投入6000万元，2012年投入8640万元．
（1）求2010年至2012年该县投入教育经费的年平均增长率；
（2）该县预计2013年投入教育经费不低于9500万元，若继续保持前两年的平均增长率，该目标能否实现？请通过计算说明理由．
某中学举行数学知识竞赛，所有参赛学生分别设有一、二、三等奖和纪念奖，获奖情况已汇制成如图所示的两幅不完整的统计图，根据图中所给信息解答下列问题：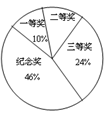
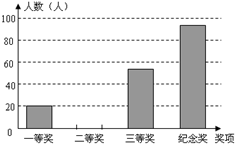
（1）这次数学知识竞赛获得二等奖人数是多少？
（2）请将条形统计图补充完整；
（3）若给所有参赛学生每人发一张卡片，各自写自己名字，然后把卡片放入一个不透明的袋子内，摇匀后任意摸取一张卡片，求摸出的卡片上是写有一等奖学生名字的概率。