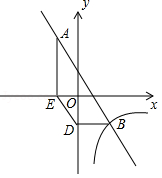
如图,在平面直角坐标系 中,抛物线 过点 ,与抛物线 的一个交点为 ,且点 的横坐标为2,点 、 分别是抛物线 、 上的动点.
(1)求抛物线 对应的函数表达式;
(2)若以点 、 、 、 为顶点的四边形恰为平行四边形,求出点 的坐标;
(3)设点 为抛物线 上另一个动点,且 平分 .若 ,求出点 的坐标.

计算: .
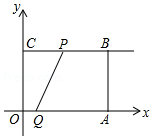
已知:如图所示,在平面直角坐标系 中,四边形 是矩形, , ,动点 从点 出发,沿射线 方向以每秒2个单位长度的速度运动;同时,动点 从点 出发,沿 轴正半轴方向以每秒1个单位长度的速度运动.设点 、点 的运动时间为 .
(1)当 时,求经过点 , , 三点的抛物线的解析式;
(2)当 时,求 的值;
(3)当线段 与线段 相交于点 ,且 时,求 的值;
(4)连接 ,当点 , 在运动过程中,记 与矩形 重叠部分的面积为 ,求 与 的函数关系式.
某电子科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元 件,在销售过程中发现:每年的年销售量 (万件)与销售价格 (元 件)的关系如图所示,其中 为反比例函数图象的一部分, 为一次函数图象的一部分.设公司销售这种电子产品的年利润为 (万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.
(1)请求出 (万件)与 (元 件)之间的函数关系式;
(2)求出第一年这种电子产品的年利润 (万元)与 (元 件)之间的函数关系式,并求出第一年年利润的最大值.
(3)假设公司的这种电子产品第一年恰好按年利润 (万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格 (元 定在8元以上 ,当第二年的年利润不低于103万元时,请结合年利润 (万元)与销售价格 (元 件)的函数示意图,求销售价格 (元 件)的取值范围.

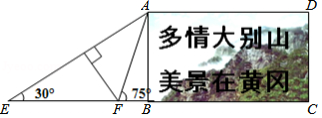
在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌 (如图所示),已知标语牌的高 ,在地面的点 处,测得标语牌点 的仰角为 ,在地面的点 处,测得标语牌点 的仰角为 ,且点 , , , 在同一直线上,求点 与点 之间的距离.(计算结果精确到0.1米,参考数据: ,
已知:如图,一次函数 与反比例函数 的图象有两个交点 和 ,过点 作 轴,垂足为点 ;过点 作 轴,垂足为点 ,且点 的坐标为 ,连接 .
(1)求 的值;
(2)求四边形 的面积.