为了庆祝六一儿童节，某食品厂制作了3种不同的精美卡片，每袋食品随机装入一张卡片，集齐三种卡片可获奖，现购买该种食品3袋，能获奖的概率是多少？
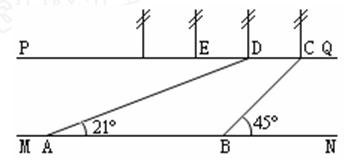
如图，南京绿博园中有一条人工河，河的两岸PQ、MN互相平行，河
岸PQ上有一排间隔为50米的彩灯柱C、D、E、……，某人在河岸MN的A处测得∠DAN＝21º，然后沿河岸走了175米到达B处，测得∠CBN＝45º，求这条河的宽度．（参考数据：
，
）
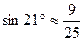统计2010年上海世博会前20天日参观人数，得到如下频数分布表和频
数分布直方图（部分未完成）：
（1）请补全频数分布表和频数分布直方图；
（2）求出日参观人数不低于22万的天数所占的百分比；
（3）利用以上信息，试估计上海世博会（会期184天）的参观总人数.
如图，在
和
中，
、
交于点M.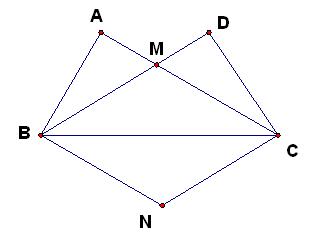
（1）求证：≌；
（2）作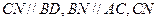
交
于点N，四边形BNCM是什么四边形？请证明你的结论.
请你先化简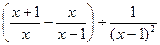
，再从0，
， 2，1中选择一
个合适的数代入，求出这个代数式的值.
