古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点 将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的一段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点 称为线段 的“黄金分割”点.如图,在 中,已知 , ,若 , 是边 的两个“黄金分割”点,则 的面积为

A. B. C. D.
-2014的相反数是()
A. |
B. |
C.2014 | D.-2014 |
己知⊙O1和⊙O2的半径分别为1和3,从如图所示位置(⊙O1与⊙O2内切)开始,将⊙O1向右平移到与⊙O2外切止,那么在这个运动过程中(包括起始位置与终止位置),圆心距O1O2的取值范围在数轴上表示正确的是()
下图表示一个正方体的展开图,下面四个正方体中只有一个符合要求,那么这个正方体是()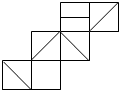
A.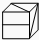 |
B.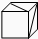 |
C. |
D. |
如图,在平面直角坐标系xOy中,直线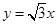 经过点A,作AB⊥x轴于点B,将△ABO绕点B顺时针旋转
经过点A,作AB⊥x轴于点B,将△ABO绕点B顺时针旋转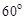 得到△BCD,若点B的坐标为(2,0),则点C的坐标为()
得到△BCD,若点B的坐标为(2,0),则点C的坐标为()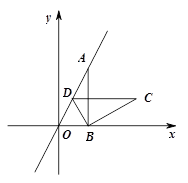
A.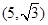 |
B.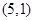 |
C.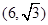 |
D.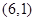 |
如图,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是()
| A.6 | B.12 | C.24 | D.48 |