如图，在矩形ABCD中，对角线相交于点O，⊙M为ΔBCD的内-优题课

游客

题文

如图，在矩形 $ABCD$ 中，对角线相交于点 $O$ ， $⊙ M$ 为 $ΔBCD$ 的内切圆，切点分别为 $N$ ， $P$ ， $Q$ ， $DN = 4$ ， $BN = 6$ ．

（1）求 $BC$ ， $CD$ ；

（2）点 $H$ 从点 $A$ 出发，沿线段 $AD$ 向点 $D$ 以每秒3个单位长度的速度运动，当点 $H$ 运动到点 $D$ 时停止，过点 $H$ 作 $HI / / BD$ 交 $AC$ 于点 $I$ ，设运动时间为 $t$ 秒．

①将 $ΔAHI$ 沿 $AC$ 翻折得△ $AH' I$ ，是否存在时刻 $t$ ，使点 $H'$ 恰好落在边 $BC$ 上？若存在，求 $t$ 的值；若不存在，请说明理由；

②若点 $F$ 为线段 $CD$ 上的动点，当 $ΔOFH$ 为正三角形时，求 $t$ 的值．

科目数学题型解答题难度较难

知识点：相似三角形的判定与性质矩形的性质翻折变换（折叠问题）切线长定理三角形的内切圆与内心

登录免费查看答案和解析

相关试题

一个不透明的口袋里装有分别标有汉字“美”、“丽”、“鄞”、“州”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．
（1）若从中任取一个球，球上的汉字刚好是“鄞”的概率为多少？
（2）甲从中任取一球，不放回，再从中任取一球，请用树状图的方法，求出甲取出的两个球上的汉字恰能组成“美丽”或“鄞州”的概率P₁；
（3）乙从中任取一球，记下汉字后再放回袋中，然后再从中任取一球，记乙取出的两个球上的汉字恰能组成“美丽”或“鄞州”的概率为P₂，指出P₁，P₂的大小关系（请直接写出结论，不必证明）．

如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？

晚上，小亮走在大街上．他发现：当他站在大街两边的两盏路灯之间，并且自己被两边路灯照在地上的两个影子成一直线时，自己右边的影子长为3米，左边的影子长为1.5米．又知自己身高1.80米，两盏路灯的高相同，两盏路灯之间的距离为12米．求路灯的高.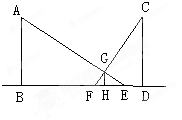

阅读理解题：
定义：如果一个数的平方等于－1，记为i²=－1，这个数i叫做虚数单位．那么和我们所学的实数对应起来就叫做复数，表示为a＋bi（a，b为实数），a叫这个复数的实部，b叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似．
例如计算：（2＋i）＋（3－4i）=（2＋3）＋（1－4）i=5－3i．
（1）填空：i³= ， i⁴= .
（2）计算：①（1＋i）（1－i）；②（1＋i）²；
（3）试一试：请利用以前学习的有关知识将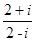化简成a＋bi的形式.

在正方形网格中建立如图所示的平面直角坐标系xoy，△ABC的三个顶点都在格点上，点A的坐标是（4，4），请解答下列问题：

（1）将△ABC向下平移5个单位长度，画出平移后的△A₁B₁C₁并写出点A的对应点A₁的坐标；
（2）画出△A₁B₁C₁关于y轴对称的△A₂B₂C₂；
（3）将△ABC绕点C逆时针旋转90°，画出旋转后的△A₃B₃C．

试卷网试题网古诗词网作文网范文网