我市东坡实验中学准备开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了 名学生(每名学生必选且只能选择这五项活动中的一种).

根据以上统计图提供的信息,请解答下列问题:
(1) , .
(2)补全上图中的条形统计图.
(3)若全校共有2000名学生,请求出该校约有多少名学生喜爱打乒乓球.
(4)在抽查的 名学生中,有小薇、小燕、小红、小梅等10名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这4名女生中,选取2名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母 、 、 、 代表)
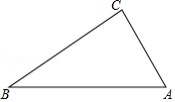
如图,在 中, , , .
(1)尺规作图:不写作法,保留作图痕迹.
①作 的平分线,交斜边 于点 ;
②过点 作 的垂线,垂足为点 .
(2)在(1)作出的图形中,求 的长.
随机抽取某小吃店一周的营业额(单位:元)如下表:
|
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
星期日 |
合计 |
|
540 |
680 |
640 |
640 |
780 |
1110 |
1070 |
5460 |
(1)分析数据,填空:这组数据的平均数是 元,中位数是 元,众数是 元.
(2)估计一个月的营业额(按30天计算)
①星期一到星期五营业额相差不大,用这5天的平均数估算合适么?
答(填“合适”或“不合适” .
②选择一个你认为最合适的数据估算这个小吃店一个月的营业额.
先化简: ,再选取一个适当的 的值代入求值.
计算: .
如图,抛物线 经过点 ,与 轴相交于 , 两点.
(1)求抛物线的函数表达式;
(2)点 在抛物线的对称轴上,且位于 轴的上方,将 沿直线 翻折得到△ ,若点 恰好落在抛物线的对称轴上,求点 和点 的坐标;
(3)设 是抛物线上位于对称轴右侧的一点,点 在抛物线的对称轴上,当 为等边三角形时,求直线 的函数表达式.
