如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形, 经过点 ,连接 交 于点 ,观察发现:点 是 的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接 交 于点 .
请参考上面的思路,证明点 是 的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当 时,延长 、 交于点 ,求 的值;
(3)在(2)的条件下,若 为大于 的常数),直接用含 的代数式表示 的值.

计算: .
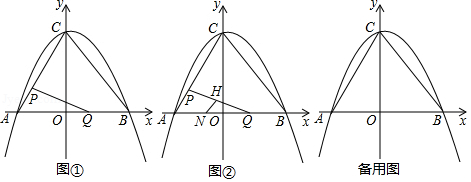
如图①,在平面直角坐标系中,二次函数 的图象与坐标轴交于 , , 三点,其中点 的坐标为 ,点 的坐标为 ,连接 , .动点 从点 出发,在线段 上以每秒1个单位长度的速度向点 作匀速运动;同时,动点 从点 出发,在线段 上以每秒1个单位长度的速度向点 作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为 秒.连接 .
(1)填空: , ;
(2)在点 , 运动过程中, 可能是直角三角形吗?请说明理由;
(3)在 轴下方,该二次函数的图象上是否存在点 ,使 是以点 为直角顶点的等腰直角三角形?若存在,请求出运动时间 ;若不存在,请说明理由;
(4)如图②,点 的坐标为 , ,线段 的中点为 ,连接 ,当点 关于直线 的对称点 恰好落在线段 上时,请直接写出点 的坐标.
(操作发现)
如图①,在边长为1个单位长度的小正方形组成的网格中, 的三个顶点均在格点上.
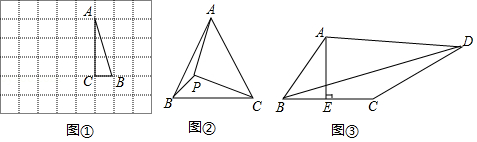
(1)请按要求画图:将 绕点 按顺时针方向旋转 ,点 的对应点为 ,点 的对应点为 ,连接 ;
(2)在(1)所画图形中, .
(问题解决)
如图②,在等边三角形 中, ,点 在 内,且 , ,求 的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将 绕点 按顺时针方向旋转 ,得到△ ,连接 ,寻找 , , 三条线段之间的数量关系;
想法二:将 绕点 按逆时针方向旋转 ,得到△ ,连接 ,寻找 , , 三条线段之间的数量关系.
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
(灵活运用)
如图③,在四边形 中, ,垂足为 , , , , 为常数),求 的长(用含 的式子表示).
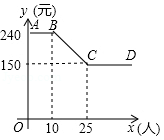
某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线 表示人均收费 (元)与参加旅游的人数 (人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为 元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?
, 两地被大山阻隔,若要从 地到 地,只能沿着如图所示的公路先从 地到 地,再由 地到 地.现计划开凿隧道 , 两地直线贯通,经测量得: , , ,求隧道开通后与隧道开通前相比,从 地到 地的路程将缩短多少?(结果精确到 ,参考数据: ,
