某公司从2013年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 |
2013 |
2014 |
2015 |
2016 |
投入技改资金 (万元) |
2.5 |
3 |
4 |
4.5 |
产品成本 (万元 件) |
7.2 |
6 |
4.5 |
4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
某市水产品市场管理部门规划建造面积为2400m2的集贸大棚,大棚内设A种类型和B种类型的店面共80间,每间A种类型的店面的平均面积为28m2,月租费为400元;每间B种类型的店面的平均面积为20m2,月租费为360元.全部店面的建造面积不低于大棚总面积的80%,又不能超过大棚总面积的85%.
(1)试确定A种类型店面的数量的范围;
(2)该大棚管理部门通过了解业主的租赁意向得知, A种类型店面的出租率为75%,B种类型店面的出租率为90%.
①开发商计划每年能有28万元的租金收入,你认为这一目标能实现吗?若能应该如何安排A、B两类店面数量?若不能,说明理由。
②为使店面的月租费最高,最高月租金是多少?
阅读理解:如图,已知直线m∥n,A、B 为直线n上两点,C、D为直线m上两点,容易证明:△ABC的面积=△ABD的面积.
根据上述内容解决以下问题:
已知正方形ABCD的边长为4,G是边CD上一点,以CG为边作正方形GCEF.
(1)如图(2), 当点G是CD的中点时,△BDF的面积为.
(2)如图(3), 当CG = a时, 则△BDF的面积为,并说明理由.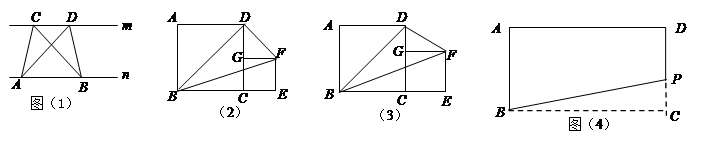
探索应用:小张家有一块长方形的土地如图(4),由于修建高速公路被占去一块三角形BCP区域.现决定在DP右侧补给小张一块土地,补偿后,土地变为四边形ABMD,要求补偿后的四边形ABMD的面积与原来形长方形ABCD的面积相等且M在射线BP上,请你在图中画出M点的位置,并简要叙述做法.
对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
(1)如果设正方形OGFN的边长为l,这七块部件的各边长中,从小到大的四个不同值分别为l、x1、x2、x3,那么x1=;各内角中最小内角是度,最大内角是度;用它们拼成的一个五边形如图②,其面积是,
(2)请用这副七巧板,既不留下一丝空白,又不相互重叠,拼出2种边数不同的凸多边形,画在下面格点图中,并使凸多边形的顶点落在格点图的小黑点上(格点图中,上下、左右相邻两点距离都为1).
注:不能拼成与图①或②全等的多边形!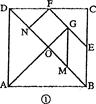


在平面直角坐标系中,已知二次函数 的图象与
的图象与 轴相交于点
轴相交于点 ,顶点为
,顶点为 ,点
,点 在这个二次函数图象的对称轴上.若四边形
在这个二次函数图象的对称轴上.若四边形 是一个边长为2且有一个内角为
是一个边长为2且有一个内角为 的菱形.求此二次函数的表达式.
的菱形.求此二次函数的表达式.
如图,“五一”节,小明和同学一起到游乐场游玩,游乐场的大型摩天轮的半径为20米,旋转1周需要24分钟(匀速)。小明乘坐最底部的车厢按逆时针方向旋转(离地面约1米)开始1周的观光。
(1)4分钟后小明离地面的高度是多少?
(2)摩天轮启动多长时间后,小明离地面的高度到达11米?
(3)在旋转一周的过程中,小明将有多长时间连续保持在离地面31米以上的空中?