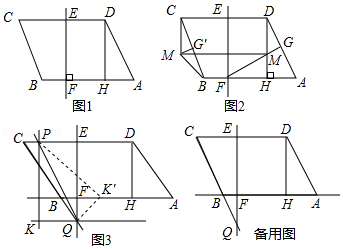
如图1,在 中, 于点 , 的垂直平分线交 于点 ,交 于点 , , , .
(1)如图2,作 于点 ,交 于点 ,将 沿 方向平移,得到△ ,连接 .
①求四边形 的面积;
②直线 上有一动点 ,求 周长的最小值.
(2)如图3,延长 交 于点 ,过点 作 ,过 边上的动点 作 ,并与 交于点 ,将 沿直线 翻折,使点 的对应点 恰好落在直线 上,求线段 的长.
)如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-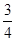 x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
(1)求抛物线的解析式;
(2)若PE =5EF,求m的值;
(3)若点E/是点E关于直线PC的对称点、是否存在点P,使点E/落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由。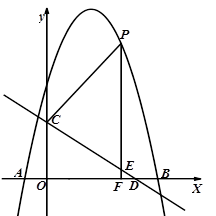
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[50°, ]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
今年,6月12日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.
(1)小华的问题解答:
(2)小明的问题解答:
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.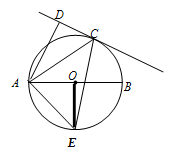
(1)求证:AC平分∠DAB;
(2)若点E为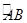 的中点,AD=
的中点,AD=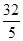 ,AC=8,求AB和AE的长.
,AC=8,求AB和AE的长.
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为时,四边形AMDN是矩形;
②当AM的值为时,四边形AMDN是菱形。