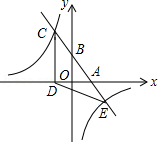
如图,一次函数 、 为常数, 的图象与 轴、 轴分别交于 、 两点,且与反比例函数 为常数,且 的图象在第二象限交于点 . 轴,垂足为 ,若 .
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为 ,求 的面积;
(3)直接写出不等式 的解集.
已知关于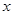 的方程
的方程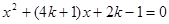 。
。(1)求证此方程一定有两个不
 相等的实数根。
相等的实数根。(2)设
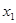 、
、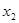 是方程的两个实数根,且(
是方程的两个实数根,且(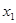 -2)(
-2)(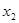 -2)=2
-2)=2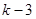 ,求
,求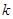 的值。
的值。
如图所示,在一 块长为32米,宽为15米的矩形草地上,在中间要设计一横二竖的等宽的、供居
块长为32米,宽为15米的矩形草地上,在中间要设计一横二竖的等宽的、供居 民散步的小路,要使小路的面积是总面积的八分之一,请问小路的宽应是多少米?
民散步的小路,要使小路的面积是总面积的八分之一,请问小路的宽应是多少米?
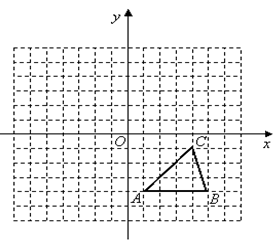
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,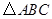 的顶点均在格点上,点
的顶点均在格点上,点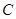 的坐标为
的坐标为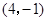 .
.
①把
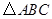 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的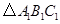 ,画出
,画出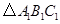 ,并写出
,并写出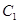 的坐标;
的坐标;②以原点
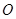 为对称中心,再画出与
为对称中心,再画出与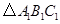 关于原点
关于原点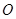 对称的
对称的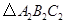 ,并写出点
,并写出点 的坐标.
的坐标.
已知a、b、c满足
求:(1)a、b、c的值;
(2)试问以a、b、c为 边能否构成三角形?若能构成三角形,求出三角形的周长;
边能否构成三角形?若能构成三角形,求出三角形的周长;
若不能构成三角形,请说明理由.
方程:
