一次函数 的图象经过点 ,且与反比例函数 的图象交于点 .
(1)求一次函数的解析式;
(2)将直线 向上平移10个单位后得到直线 , 与反比例函数 的图象相交,求使 成立的 的取值范围.
小明带着580元去买饮水机,看到甲﹑乙两家超市一款相同型号的饮水机,且标价相同,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价的8折优惠;在乙超市满200返50现金,满400返100现金,满600返150现金,…依次类推.假设小明预计购买的饮水机标价为x元.(0≤x<600)
(1)请用含x的代数式分别表示小明在两家超市购买饮水机应付的现金,
(2)若饮水机的标价为380元,试比较小明到哪家超市购买更优惠?
(3)请你帮小明算算:若他付460元现金,在两家超市购买的饮水机标价分别为多少?
若代数式 且
且 求
求 的值.
的值.
已知多项式x 与bx
与bx 的差的值与x的值无关,求代数式3(a
的差的值与x的值无关,求代数式3(a 的值.
的值.
某人买了50元的乘车月票卡,如果此人乘车的次数用m表示,则记录他每次乘车后的余额n元如下表: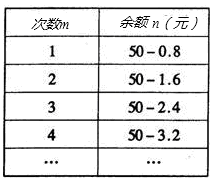
(1)请你写出此人乘车的次数m表示余额n的公式;
| 次数m |
余额n元 |
| 1 |
50-0.8 |
| 2 |
50-1.6 |
| 3 |
50-2.4 |
| 4 |
50-3.2 |
| … |
… |
(2)求当m=13时,他的余额是多少元?
(3)问此人最多能乘多少次车?
根据下面的俯视图,其搭建的每一正方体边长为2cm,画出它的主视图和左视图,并求其表面积.